题目内容
(本小题满分12分)
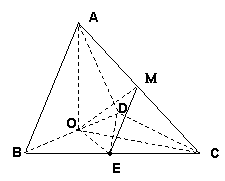
如图,四面体ABCD中,O、E分别是BD、BC的中点,![]()
(Ⅰ) 求证:![]() 平面BCD;
平面BCD;
(Ⅱ) 求异面直线AB与CD所成角余弦的大小;
(Ⅲ) 求点E到平面ACD的距离.
 |
解:(1) 证明:连结OC,
![]()
![]()
![]() ,
,![]() .
.
在![]() 中,由已知可得
中,由已知可得![]() …………3分
…………3分
而![]() , ∴
, ∴![]()
∴![]() 即
即![]()
![]() ∴
∴![]() 平面
平面![]() . …………… 4分
. …………… 4分
(2) 解:以O为原点,如图建立空间直角坐标系,
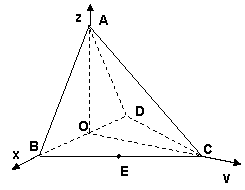 则
则![]()
![]()
![]()
∴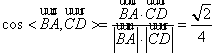 ,
,
∴ 异面直线AB与CD所成角余弦的大小为![]() .…… 8分
.…… 8分
(3) 解:设平面ACD的法向量为![]() 则
则
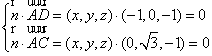 ,∴
,∴  ,
,
令![]() 得
得![]() 是平面ACD的一个法向量. 又
是平面ACD的一个法向量. 又![]()
∴点E到平面ACD的距离 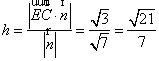 .……… 12分
.……… 12分
(3) (法二)解:设点E到平面ACD的距离为![]() .
.
![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,
,
∴![]() ,而
,而![]() ,
,![]() .
.
∴ , ∴点E到平面ACD的距离为
, ∴点E到平面ACD的距离为![]() …………… 12分
…………… 12分

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目