题目内容
已知函数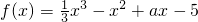 在区间[-1,2]上单调递减,则实数a的取值范围为
在区间[-1,2]上单调递减,则实数a的取值范围为
- A.(-∞,+∞)
- B.[1,+∞)
- C.(-3,1)
- D.(-∞,-3]
D
分析:求出函数的单调区间,由于函数在[-1,2]上单调递减,故此区间是其定义上单调区间的子集,故比较区间的端点即可得到参数的取值范围,选出正确答案.
解答:函数的导数为f'(x)=x2-2x+a,判断知△=4-4a>0.得a<1
相应方程的根为x=
令f′(x)=x2-2x+a<0,解得 ,即函数在
,即函数在 上是减函数,
上是减函数,
又函数在区间[-1,2]上单调递减,
∴ ,解得a≤-3
,解得a≤-3
综上得实数a的取值范围为(-∞,-3]
故选D
点评:本题考查利用导数研究函数的单调性,求解本题的关键是利用导数求出函数的单调递减区间以及根据题设条件作出正确判断得出参数所满足的不等式,解出参数的取值范围,根据题设转化出不等式是本题的易错点,要注意等价转化.
分析:求出函数的单调区间,由于函数在[-1,2]上单调递减,故此区间是其定义上单调区间的子集,故比较区间的端点即可得到参数的取值范围,选出正确答案.
解答:函数的导数为f'(x)=x2-2x+a,判断知△=4-4a>0.得a<1
相应方程的根为x=

令f′(x)=x2-2x+a<0,解得
 ,即函数在
,即函数在 上是减函数,
上是减函数,又函数在区间[-1,2]上单调递减,
∴
 ,解得a≤-3
,解得a≤-3综上得实数a的取值范围为(-∞,-3]
故选D
点评:本题考查利用导数研究函数的单调性,求解本题的关键是利用导数求出函数的单调递减区间以及根据题设条件作出正确判断得出参数所满足的不等式,解出参数的取值范围,根据题设转化出不等式是本题的易错点,要注意等价转化.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为 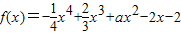 在区间[-1,1]上单调递减,在区间[1,2]上单调递增,
在区间[-1,1]上单调递减,在区间[1,2]上单调递增,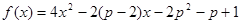 在区间[-1,1]上至少存在一个实数c使f(c)>0,则实数p的范围 .
在区间[-1,1]上至少存在一个实数c使f(c)>0,则实数p的范围 . 在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为