题目内容

已知圆锥曲线mx2+4y2=4m的离心率e为方程2x2-5x+2=0的两根，则满足条件的圆锥曲线的条数为（　　）
A．1B．2C．3D．4
方程2x2-5x+2=0的根是
1
2
和2
当e=
1
2
时圆锥曲线mx2+4y2=4m是椭圆，当e=2时圆锥曲线mx2+4y2=4m是双曲线．
x2
4
+
y2
m
=1，
若
x2
4
+
y2
m
=1，是椭圆，则c2=|4-m|，
e=
c
a
=
|4-m|
2
=
1
2
或
4-m|
m
=
1
2
，满足条件的圆锥曲线有2个；
若
x2
4
+
y2
m
=1是双曲线，则m＜0
所以c2=4-m
e=
4-m
2
=2，满足条件的圆锥曲线有1个．
所以满足条件的圆锥曲线一共3条．
故选C．
练习册系列答案
相关题目
如果方程
x2
|m|-1
-
y2
m-2
=1表示双曲线，那么实数m的取值范围是______．
双曲线
x2
4
-
y2
k
=1的离心率e∈（1，2），则k的取值范围是______．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线方程为y=±2x，则其离心率为（　　）
A．5B．
5
2
C．
3
D．
5
双曲线
x2
a2
-
y2
b2
=1的两焦点分别为F1和F2，若双曲线上存在不是顶点的点P，使得∠PF2F1=3∠PF1F2，则双曲线离心率e的取值范围是______．
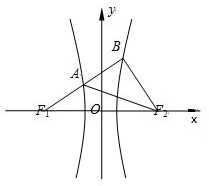
如图，F1，F2是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，过F1的直线l与C的左、右分支分别交于A，B两点．若AB：BF2：AF2=3：4：5，则双曲线的离心率为______．
双曲线
x2
a2
-
y2
b2
=1（a＞1，b＞0）的焦点距为2c，直线l过点（a，0）和（0，b），且点（1，0）到直线l的距离与点（-1，0）到直线l的距离之和s≥
4
5
c．求双曲线的离心率e的取值范围．
若双曲线
x2
16
-
y2
m
=1的焦距为10，则双曲线的渐近线方程为______．
设F1、F2是双曲线
x2
16
-
y2
20
=1的左右焦点，点P在双曲线上，若点P到左焦点F1的距离等于9，则点P到右准线的距离（　　）
A．
2
3
B．
34
3
C．
2
3
或
34
3
D．
51
2
或
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网