Question

一个正三棱锥P-ABC的三视图如图所示，尺寸单位：cm．求：
（1）正三棱锥P-ABC的表面积；    
（2）正三棱锥P-ABC的体积．

Answer 1

分析：（1）由三视图判断几何体为正三棱锥，且底面是边长为12的等边三角形，高为2

3

，结合图形求出斜高，进而求得侧面积与底面面积之和．
（2）代入棱锥的体积公式计算可得答案．

解答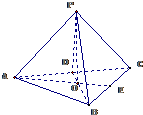：解：（1）由三视图判断几何体为底面是边长为12的等边三角形，高为2

3

的正三棱锥，其直观图如图：．
底面边长AB=BC=CA=12⇒BD=6

3

．
∵三棱锥P-ABC为正三棱锥，∴O为底面正三角形的中心，
∴DO=

1

3

BD=2

3

，∴斜高PD=

12+12

=2

6

∴侧面面积为3×

1

2

×AC×PD=36

6

（cm²），
底面面积为

1

2

×12×12×

3

2

=

3

4

×12²=36

3

（cm²）
∴正三棱锥P-ABC的表面积为36

6

+36

3

（cm²）；
（2）正三棱锥P-ABC的体积V=

1

3

×

1

2

×12×12×

3

2

×2

3

=

1

3

×36

3

×2

3

=72 （cm³）

点评：本题考查了由三视图求几何体的表面积与体积，根据三视图还原其直观图是解答本题的关键．