题目内容
6.化简:$\frac{sin(π+α)cos(2π+α)}{sin(-α-π)cos(-π+α)}$=1.分析 利用三角函数的诱导公式进行化简即可.
解答 解:$\frac{sin(π+α)cos(2π+α)}{sin(-α-π)cos(-π+α)}$=$\frac{-sinαcosα}{-sin(α+π)cos(π-α)}$=$\frac{-sinαcosα}{-sinαcosα}$=1,
故答案为:1.
点评 本题主要考查三角函数值的化简和求值,利用三角函数的诱导公式是解决本题的关键,比较基础.

练习册系列答案
相关题目
5.已知$α∈[{π,\frac{3π}{2}}]$,$sinα=-\frac{3}{5}$,则tanα=( )
| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |

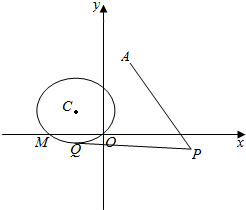 圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.
圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.