题目内容
设f（x）=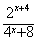
。
（1）求f（x）的最大值；
（2）证明：对任意实数a、b恒有f（a）＜b2-3b+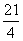
。
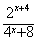。（1）求f（x）的最大值；
（2）证明：对任意实数a、b恒有f（a）＜b2-3b+
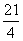。解：（1）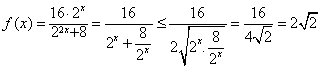
当且仅当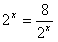
时，即
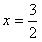时，等号成立
∴f（x）的最大值为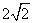
；
（2）
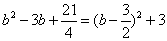
∴当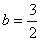
时，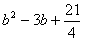
有最小值3，由（1）知f（a）有最大值2
，且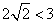
∴对任意实数a，b都有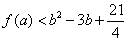
。
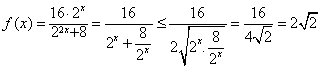
当且仅当
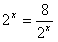时，即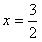时，等号成立∴f（x）的最大值为
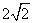；（2）
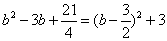
∴当
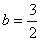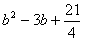时，有最小值3，由（1）知f（a）有最大值2，且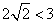∴对任意实数a，b都有
。
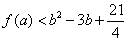练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目