题目内容
(本小题满分12分)
已知常数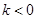 ,函数
,函数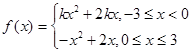
(1)求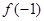 ,
,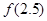 的值;
的值;
(2)讨论函数 在
在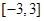 上的单调性;
上的单调性;
(3)求出 在
在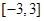 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
(1)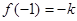 ,
,
(2)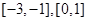 上为增函数,在
上为增函数,在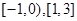 上为减函数
上为减函数
(3)① 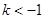 时,
时, 在
在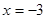 处取得最小值
处取得最小值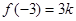 ,在
,在 处取得最大值
处取得最大值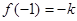
②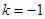 时,
时, 在
在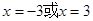 处取得最小值
处取得最小值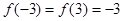 ,
,
在 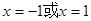 处取得最大值
处取得最大值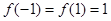
③ 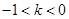 时,
时, 在
在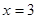 处取得最小值
处取得最小值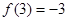 ,在
,在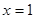 处取得最大值
处取得最大值 .
.
解析试题分析:(1)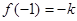 ,
,
(2)∵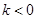 ,∴
,∴ 在
在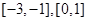 上为增函数,在
上为增函数,在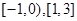 上为减函数
上为减函数
(3)由函数 在
在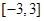 上的单调性可知,
上的单调性可知, 在
在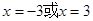 处取得最小值
处取得最小值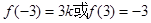 ,而在
,而在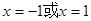 处取得最大值
处取得最大值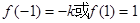
故有
① 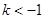 时,
时, 在
在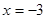 处取得最小值
处取得最小值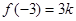 ,在
,在 处取得最大值
处取得最大值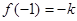
②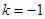 时,
时, 在
在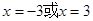 处取得最小值
处取得最小值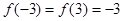 ,
,
在 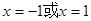 处取得最大值
处取得最大值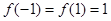
③ 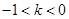 时,
时, 在
在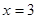 处取得最小值
处取得最小值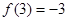 ,在
,在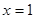 处取得最大值
处取得最大值 .
.
考点:本题主要考查分段函数的概念,二次函数的最值,分类讨论思想。
点评:中档题,二次函数的最值问题,往往有“轴定区间动”、“轴动区间定”等不同情况,关键是讨论对称轴与给定区间的相对位置。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
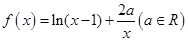
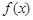 的单调区间;
的单调区间;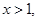 且
且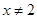 时,
时,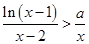 恒成立,求实数
恒成立,求实数 的范围.
的范围.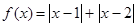 .
.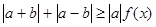 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.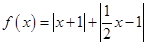 .
.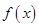 的图象,写出函数
的图象,写出函数 的不等式
的不等式
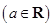 .
.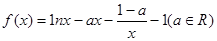 .
.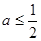 时,讨论
时,讨论 的单调性;
的单调性;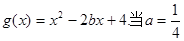 时,若对任意
时,若对任意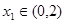 ,存在
,存在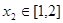 ,使
,使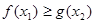 ,求实数
,求实数 的取值范围.
的取值范围. 元,若销售价为
元,若销售价为 元,可卖出
元,可卖出 元,销售量就减少
元,销售量就减少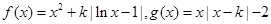 ,其中
,其中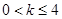 .(1) 讨论函数
.(1) 讨论函数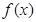 的单调性,并求出
的单调性,并求出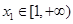 ,都存在
,都存在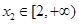 ,使得
,使得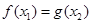 ,求实数
,求实数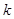 的取值范围.
的取值范围.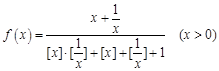 ,其中
,其中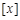 表示不超过
表示不超过 的最大整数,如
的最大整数,如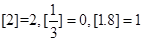 .
.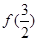 的值;
的值;  上存在x,使得
上存在x,使得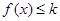 成立,求实数k的取值范围;
成立,求实数k的取值范围; 的值域.
的值域. 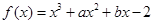 的图象过点
的图象过点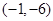 ,且函数
,且函数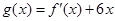 的图象关于
的图象关于 轴对称;
轴对称;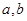 的值及函数
的值及函数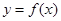 的单调区间;
的单调区间;