题目内容
对于幂函数f(x)= ,若0<x1<x2,则
,若0<x1<x2,则 ,
, 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D.无法确定 |
A
解析试题分析:可以根据幂函数f(x)= 在(0,+∞)上是增函数,函数的图象是上凸的,则当0<x1<x2时,应有
在(0,+∞)上是增函数,函数的图象是上凸的,则当0<x1<x2时,应有 >
> ,由此可得结论.
,由此可得结论.
考点:函数的性质的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若不等式 对任意不大于1的实数x和大于1的正整数n都成立,则
对任意不大于1的实数x和大于1的正整数n都成立,则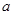 的取值范围是( )
的取值范围是( )
A.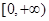 | B.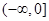 | C.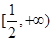 | D.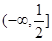 |
设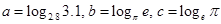 ,则( )
,则( )
A. | B. | C. | D. |
若 ,则有( ).
,则有( ).
A.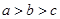 | B. | C. | D. |
某车间分批生产某种产品,每批的生产准备费用为800元,若每批生产x件,则平均仓储时间为 天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品 ( ).
天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品 ( ).
| A.60件 | B.80件 |
| C.100件 | D.120件 |
设a>0,b>0,e是自然对数的底数( )
| A.若ea+2a=eb+3b,则a>b |
| B.若ea+2a=eb+3b,则a<b |
| C.若ea-2a=eb-3b,则a>b |
| D.若ea-2a=eb-3b,则a<b |
知函数y=f(x)的值域为C,若函数x=g(t)使函数y=f[g(t)]的值域仍为C,则称x=g(t)是y=f(x)的一个等值域变换,下列函数中,x=g(t)是y=f(x)的一个等值域变换的为( )
A.f(x)=2x+b,x∈R,x= |
| B.f(x)=ex,x∈R,x=cost |
| C.f(x)=x2,x∈R,x=et |
| D.f(x)=|x|,x∈R,x=lnt |
某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是( )
| A.118元 | B.105元 |
| C.106元 | D.108元 |
函数f(x)=|x-2|-lnx在定义域内零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |