题目内容
设a、b∈R，i为虚数单位，若（a+i）i=b+i，则复数z=a+bi的模为 ．
【答案】分析：把给出的等式左边采用单项式乘以多项式展开，然后利用复数相等的概念得到a，b的值，最后利用复数模的公式求模．
解答：解：由（a+i）i=b+i，得-1+ai=b+i，
所以a=1，b=-1．
则z=1-i．
所以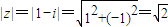
．
故答案为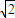
．
点评：本题考查了复数相等的条件，考查了复数模的求法，两个复数相等，当且仅当实部等于实部，虚部等于虚部，是基础题．
解答：解：由（a+i）i=b+i，得-1+ai=b+i，
所以a=1，b=-1．
则z=1-i．
所以
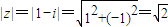．故答案为
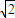．点评：本题考查了复数相等的条件，考查了复数模的求法，两个复数相等，当且仅当实部等于实部，虚部等于虚部，是基础题．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
关于复数z=
，下列说法中正确的是（ ）
| (1+i)2 |
| 1-i |
| A、在复平面内复数z对应的点在第一象限 | ||
B、复数z的共轭复数
| ||
| C、若复数z1=z+b（b∈R）为纯虚数，则b=1 | ||
| D、设a，b为复数z的实部和虚部，则点（a，b）在以原点为圆心，半径为1的圆上 |
恒成立
，若
i
[