题目内容
已知函数f(x)=loga 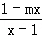 (a>0,a≠1)的图象关于原点对称.
(a>0,a≠1)的图象关于原点对称.
(1)求m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(t,a)时,f(x)的值域是(1,+∞)求a与t的值.
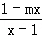 (a>0,a≠1)的图象关于原点对称.
(a>0,a≠1)的图象关于原点对称.(1)求m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(t,a)时,f(x)的值域是(1,+∞)求a与t的值.
解:(1)因为函数f(x)=loga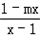 (a>0,a≠1)的图象关于原点对称,即f(x)为奇函数,则
(a>0,a≠1)的图象关于原点对称,即f(x)为奇函数,则
f(﹣x)+f(x)=0,
loga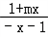 +loga
+loga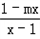 =loga
=loga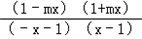 =0,
=0,
即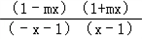 =1,
=1,
解可得,m=1或m=﹣1,
当m=1时,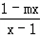 =﹣1<0,不合题意,舍去;
=﹣1<0,不合题意,舍去;
当m=﹣1时, =
=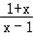 ,符合题意,
,符合题意,
故m=﹣1;
(2)当0<a<1时,loga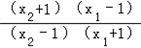 >0,即f(x2)﹣f(x1)>0,
>0,即f(x2)﹣f(x1)>0,
此时f(x)为增函数,
当a>1时,loga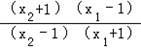 <0,即f(x2)﹣f(x1)<0,
<0,即f(x2)﹣f(x1)<0,
此时f(x)为减函数,证明如下
由(1)得m=﹣1,则f(x)=loga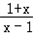 ,任取1<x1<x2,则
,任取1<x1<x2,则
f(x2)﹣f(x1)=loga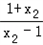 ﹣loga
﹣loga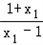 =loga
=loga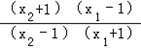 ,
,
又由1<x1<x2,则0<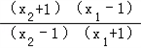 <1,
<1,
当0<a<1时,loga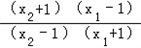 >0,即f(x2)﹣f(x1)>0,
>0,即f(x2)﹣f(x1)>0,
此时f(x)为增函数,
当a>1时,loga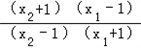 <0,即f(x2)﹣f(x1)<0,
<0,即f(x2)﹣f(x1)<0,
此时f(x)为减函数,
(3)由(1)知,f(x)=loga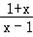 ,
,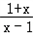 >0,解可得,x>1或x<﹣1,则
>0,解可得,x>1或x<﹣1,则
f(x)的定义域为(﹣∞,﹣1)∪(1,+∞),
故(t,a)必然含于(﹣∞,﹣1)或(1,+∞),
由a>1,可知(t,a)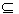 (- ∞,﹣1)不成立,则必有(t,a)
(- ∞,﹣1)不成立,则必有(t,a)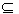 (1,+∞),
(1,+∞),
此时,f(x)的值域为(1,+∞),
又由函数f(x)为减函数,必有f(a)=1且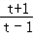 =0;
=0;
解可得,t=﹣1,a=1+ ;
;
故t=﹣1,a=1+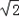 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目