题目内容
(2009•虹口区二模)已知函数f (x)=
(1)判断f (x)在区间(0,+∞)上的单调性,并证明;
(2)若关于x的方程f (x)=k有根在[2,3]内,求实数k的取值范围;
(3)若关于x的方程f (x)=k x2有四个不同的实数根,求实数k的取值范围.
| |x| | x+2 |
(1)判断f (x)在区间(0,+∞)上的单调性,并证明;
(2)若关于x的方程f (x)=k有根在[2,3]内,求实数k的取值范围;
(3)若关于x的方程f (x)=k x2有四个不同的实数根,求实数k的取值范围.
分析:(1)当x>0时,f (x)=
=
=1-
,利用单调性的定义设0<x1<x2,判定f(x1)与f(x2)的大小即可
(2)当x∈[2,3]时,f(x)=
=1-
结合x∈[2,3]可求f(x)的范围,若f(x)=k在[2,3]上有解,则f(x)的范围即是k的范围
(3)f(x)=kx2有四个根,即
=kx2(*)有四个根,当x=0时,是方程(*)的1个根,则只要
=kx2有3个不为0的根,而
=
结合函数g(x)=
的图象可求
| |x| |
| x+2 |
| x |
| x+2 |
| 2 |
| x+2 |
(2)当x∈[2,3]时,f(x)=
| x |
| x+2 |
| 2 |
| 2+x |
(3)f(x)=kx2有四个根,即
| |x| |
| x+2 |
| |x| |
| x+2 |
| 1 |
| k |
|
|
解答:解:(1)当x>0时,f (x)=
=
=1-
设0<x1<x2
∴f(x1)-f(x2)=1-
-1+
=
-
=
∵0<x1<x2
∴2(x1-x2)<0,(2+x1)(2+x2)>0
∴
<0
∴f(x1)<f(x2)
∴函数f(x)在(0,+∞)单调递增
(2)当x∈[2,3]时,f(x)=
=1-
∴4≤2+x≤5,
≤
≤
∴
≤1-
≤
∵f(x)=k在[2,3]上有解,则
≤k≤
(3)f(x)=kx2有四个根,即
=kx2(*)有四个根
当x=0时,是方程(*)的1个根
则
=kx2有3个不为0的根
而
=
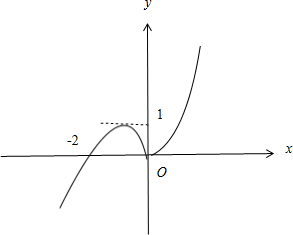
结合函数g(x)=
的图象可知满足条件时有0<
<1
∴k>1
| |x| |
| x+2 |
| x |
| x+2 |
| 2 |
| x+2 |
设0<x1<x2
∴f(x1)-f(x2)=1-
| 2 |
| 2+x1 |
| 2 |
| 2+x2 |
=
| 2 |
| 2+x2 |
| 2 |
| 2+x1 |
| 2(x1-x2) |
| (2+x1)(2+x2) |
∵0<x1<x2
∴2(x1-x2)<0,(2+x1)(2+x2)>0
∴
| 2(x1-x2) |
| (2+x1)(2+x2) |
∴f(x1)<f(x2)
∴函数f(x)在(0,+∞)单调递增
(2)当x∈[2,3]时,f(x)=
| x |
| x+2 |
| 2 |
| 2+x |
∴4≤2+x≤5,
| 2 |
| 5 |
| 2 |
| 2+x |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 2+x |
| 3 |
| 5 |
∵f(x)=k在[2,3]上有解,则
| 1 |
| 2 |
| 3 |
| 5 |
(3)f(x)=kx2有四个根,即
| |x| |
| x+2 |
当x=0时,是方程(*)的1个根
则
| |x| |
| x+2 |
而
| 1 |
| k |
|
|
| 1 |
| k |
∴k>1

点评:本题主要考查了函数的单调性的判断,函数值域的求解,方程的根与函数交点的相互转化,体现了分类讨论、转化思想与数形结合思想在解题中的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目