题目内容
若直角坐标平面内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则答点对(P,Q)是函数y=f(x)的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数f(x)=
,则此函数的“友好点对”有
|
2
2
对.分析:根据题意:“友好点对”,可知,欲求f(x)的“友好点对”,只须作出函数y=-2x2+4x-1(x≥0)的图象关于原点对称的图象,看它与函数y=-
(x<0)的图象的交点个数即可.
| 2 x |
| 3 |
解答:解:根据题意:“友好点对”,可知,
作出函数y=-2x2+4x-1(x≥0)的图象关于原点对称的图象,
同一坐标系里作出函数y=-
的图象如下图:

观察图象可得,它们在x<0时的交点为A、B,个数是2.
即f(x)的“友好点对”有:2个.
故答案为:2.
作出函数y=-2x2+4x-1(x≥0)的图象关于原点对称的图象,
同一坐标系里作出函数y=-
| 2 x |
| 3 |

观察图象可得,它们在x<0时的交点为A、B,个数是2.
即f(x)的“友好点对”有:2个.
故答案为:2.
点评:本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,属于基础题.解答的关键在于对“友好点对”的正确理解,合理地利用图象法解决.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
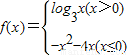 ,此函数的“友好点对”有 .
,此函数的“友好点对”有 .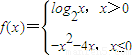 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )