题目内容
已知函数
是奇函数，且f（a2-2a）＞f（3），则实数a的取值范围是________．
（-∞，-1）∪（3，+∞）
分析：由奇函数的性质可知，f（0）=0，代入可求m，然后结合函数f（x）的单调性可得a2-2a与3的大小，从而可求a的范围
解答：由奇函数的性质可知，f（0）=0
即
∴m=0，f（x）=
=1-
在R上单调递增
∵f（a2-2a）＞f（3）
∴a2-2a＞3
即a2-2a-3＞0解不等式可得，a＞3或a＜-1
故答案为：（-∞，-1）∪（3，+∞）
点评：本题主要考查了奇函数性质的应用及利用函数的单调性求解不等式的应用．
分析：由奇函数的性质可知，f（0）=0，代入可求m，然后结合函数f（x）的单调性可得a2-2a与3的大小，从而可求a的范围
解答：由奇函数的性质可知，f（0）=0
即
∴m=0，f（x）=
=1-在R上单调递增∵f（a2-2a）＞f（3）
∴a2-2a＞3
即a2-2a-3＞0解不等式可得，a＞3或a＜-1
故答案为：（-∞，-1）∪（3，+∞）
点评：本题主要考查了奇函数性质的应用及利用函数的单调性求解不等式的应用．
练习册系列答案
相关题目
是奇函数，且
，
的值；
在区间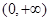
上是减函数. 
是奇函数，且在区间
上单调递减，则
上是（ ） 
B. 单调递减函数，且有最大值
D.
单调递增函数，且有最大值
是奇函数，且
.
上的单调性，并加以证明. 
是奇函数，且图像在点
为自然对数的底数）处的切线斜率为3.
、
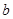的值;
，且
对任意
恒成立，求
的最大值;
时，证明：
是奇函数，且满足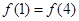
、
的值；
在区间
单调递减，在区间
单调递增；
同时满足以下两个条件：1不等式
对
恒成立；
2方程
在
上有解．若存在，试求出实数