Question

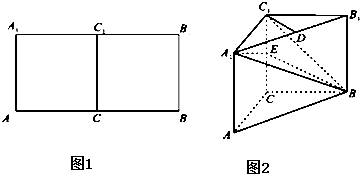
在长方形中，，，分别是，的中点（如左图）.将此长方形沿对折，使平面平面（如右图），已知，分别是，的中点.

（Ⅰ）求证：∥平面；

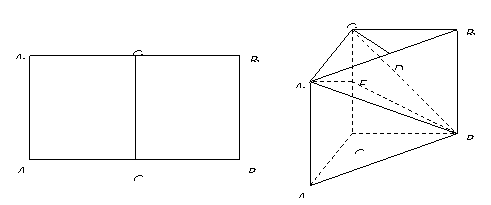
（Ⅱ）求证：平面平面；

（Ⅲ）求三棱锥的体积.

Answer 1

【解析】（Ⅰ）取的中点，连接，.   ……………1分

因为，分别是，的中点

    所以是△的中位线.    ……………2分

    所以∥∥，且.

    又因为是的中点，

    所以.

    所以∥，且.

    所以四边形是平行四边形.   …………3分

    所以∥.

    又平面，平面，    …………………………………4分

   所以∥平面.             ……………………………………………5分

（Ⅱ）因为，，且，

所以平面.         

    因为∥，所以平面.

    因为平面，所以.    …………………………………6分

    又因为，且是的中点， 所以.  ………………7分

    因为，所以平面.     …………………………8分

    由（Ⅰ）知∥，

    所以平面.

    又因为平面，

   所以平面平面.       …………………………………………10分

解：（Ⅲ）由已知，长方形沿对折后，.

    所以.

    所以，且，.

    所以平面.

    即平面.         ……………………………………………………11分

    所以.     ……………………………………12分

    其中.

   所以.   ………………………13分