题目内容
若关于x的方程
=k(x-2)+3有两个不等实数根，则实数k的范围是（ ）
| 4-x2 |
分析：由题意构造一段圆弧x2+y2=4 （y≥0），与直线y=kx+3-2k，通过直线恒过定点（2，3），考虑直线与圆相切及过点（-2，0）两个位置的斜率，从而得解．
解答：
解：由题意，等式左边是一段圆弧x2+y2=4 （y≥0）
右边是条直线y=kx+3-2k，直线恒过定点（2，3）．
根据点到直线的距离小于半径时才有和圆弧所在的圆有两个交点．
∴k＞
当直线过点（-2，0）时，k=
，
所以方程
=k(x-2)+3有两个不等实根时，
＜k≤
．
故选A．
解：由题意，等式左边是一段圆弧x2+y2=4 （y≥0）右边是条直线y=kx+3-2k，直线恒过定点（2，3）．
根据点到直线的距离小于半径时才有和圆弧所在的圆有两个交点．
∴k＞
| 5 |
| 12 |
当直线过点（-2，0）时，k=
| 3 |
| 4 |
所以方程
| 4-x2 |
| 5 |
| 12 |
| 3 |
| 4 |
故选A．
点评：本题以方程根为载体，考查根的存在性及根的个数判断，其中利用方程的几何意义，是解答本题的关键．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
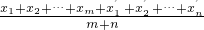的值为
的值为（ ）
的值为（ ）
