题目内容
已知函数f(x)=ax- 的反函数f-1(x)的图象过点(-1,2),且函数f(x)为减函数.
的反函数f-1(x)的图象过点(-1,2),且函数f(x)为减函数.
(1)求y=f-1(x)的解析式;
(2)求满足f-1(2x)>f-1(x2+1)的x的取值范围.
解:(1)∵反函数f-1(x)的图象过点(-1,2),
故函数f(x)的图象过点(2,-1),∴-1=a2- ,解得a=3,或a=
,解得a=3,或a= .
.
又f(x)为减函数,∴a= ,所以f(x)=
,所以f(x)=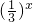 -
- ,f(x)>-
,f(x)>- .
.
所以f-1(x)=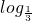 (x+
(x+ ),(x>-
),(x>- ).
).
(2)由f-1(2x)>f-1(x2+1),可得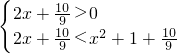 ,解得
,解得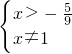 .
.
故满足f-1(2x)>f-1(x2+1)的x的取值范围是{x|x>- 且x≠1}.
且x≠1}.
分析:(1)由题意可得函数f(x)的图象过点(2,-1),解得a的值,求出函数f(x)的解析式,从而得到 f-1(x)的解析式.
(2)由f-1(2x)>f-1(x2+1)可得,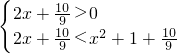 ,由此求出x的取值范围.
,由此求出x的取值范围.
点评:本题主要考查对数函数的单调性和特殊点,求一个函数的反函数,属于基础题.
故函数f(x)的图象过点(2,-1),∴-1=a2-
 ,解得a=3,或a=
,解得a=3,或a= .
.又f(x)为减函数,∴a=
 ,所以f(x)=
,所以f(x)=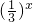 -
- ,f(x)>-
,f(x)>- .
.所以f-1(x)=
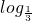 (x+
(x+ ),(x>-
),(x>- ).
).(2)由f-1(2x)>f-1(x2+1),可得
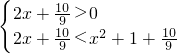 ,解得
,解得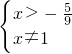 .
.故满足f-1(2x)>f-1(x2+1)的x的取值范围是{x|x>-
 且x≠1}.
且x≠1}.分析:(1)由题意可得函数f(x)的图象过点(2,-1),解得a的值,求出函数f(x)的解析式,从而得到 f-1(x)的解析式.
(2)由f-1(2x)>f-1(x2+1)可得,
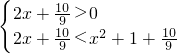 ,由此求出x的取值范围.
,由此求出x的取值范围.点评:本题主要考查对数函数的单调性和特殊点,求一个函数的反函数,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目