题目内容
已知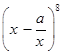
展开式中常数项为5670，其中
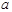是常数，则展开式中各项系数的和是( )
| A．28 | B．48 | C．28或48 | D．1或28 |
C
解析试题分析：
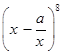，因为展开式中常数项为
，令
，
，
，解得
，当
时，令
得展开式中各项系数的和为
，当
时，令得展开式中各项系数的和为
．
考点：二项式定理．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
三名学生与两名老师并排站成一排。如果老师甲必须排在老师乙的左边，且两名老师必须相邻，那么不同的排法共有（ ）种.
| A．60 | B．48 | C．36 | D．24 |
六张卡片上分别写有数字1，1，2，3，4，5，从中取四张排成一排，可以组成不同的四位奇数的个数为（ ）
| A．180 | B．126 | C．93 | D．60 |
已知集合A＝{x|x＝a0＋a1×3＋a2×32＋a3×33}，其中ak∈{0,1,2}(k＝0,1,2,3)，且a3≠0，则A中所有元素之和等于( )
| A．3 240 | B．3 120 |
| C．2 997 | D．2 889 |
在
5的二项展开式中，x的系数为( )．
| A．10 | B．－10 | C．40 | D．－40 |
某市教育局人事部门打算将甲、乙、丙、丁四名应届大学毕业生安排到该市三所不同的学校任教，每所学校至少安排一名，其中甲、乙因属同一学科，不能安排在同一所学校，则不同的安排方法种数为( )．
| A．18 | B．24 | C．30 | D．36 |
某高校从5名男大学生志愿者和4名女大学生志愿者中选出3名派到3所学校支教(每所学校一名志愿者)，要求这3名志愿者中男、女大学生都有，则不同的选派方案共有 ( )．
| A．210种 | B．420种 |
| C．630种 | D．840种 |
若
4＝a＋b
(a，b为有理数)，则a＋b＝( )．
| A．36 | B．46 | C．34 | D．44 |