题目内容
对于函数①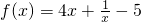 ,②
,②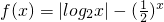 ,③f(x)=cos(x+2)-cosx,
,③f(x)=cos(x+2)-cosx,
判断如下两个命题的真假:
命题甲:f(x)在区间(1,2)上是增函数;
命题乙:f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.
能使命题甲、乙均为真的函数的序号是
- A.①
- B.②
- C.①③
- D.①②
D
分析:①函数可用导数求出在(1,2)上是增函数,②函数是|log2x|与- 的和函数,且两者在区间(1,2)上均是增函数,知
的和函数,且两者在区间(1,2)上均是增函数,知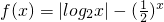 是增函数.③f(x)=0得cos(x+2)=cosx,在(0,+∞)上无数个零点.
是增函数.③f(x)=0得cos(x+2)=cosx,在(0,+∞)上无数个零点.
解答:①f'(x)=4- ,在区间(1,2)f'(x)>0,f(x)在区间(1,2)上是增函数.使甲为真.f(x)的最小值是-1<0当x=
,在区间(1,2)f'(x)>0,f(x)在区间(1,2)上是增函数.使甲为真.f(x)的最小值是-1<0当x= 时取得.又f(1)=0,∴f(x)在区间(0,+∞)上恰有两个零点x1<
时取得.又f(1)=0,∴f(x)在区间(0,+∞)上恰有两个零点x1< ;x2=1. x1x2=x1<1,使乙为真.
;x2=1. x1x2=x1<1,使乙为真.
②在区间(1,2),|log2x|=log2x,是增函数.- 也是增函数,两者的和函数也是增函数.使甲为真.利用信息技术f(x)在区间(0,+∞)上恰有两个零点x1,x2;0<x1<
也是增函数,两者的和函数也是增函数.使甲为真.利用信息技术f(x)在区间(0,+∞)上恰有两个零点x1,x2;0<x1<
1<x2<2.使乙为真.
③f(x)=0得cos(x+2)=cosx.x+2=2kπ±x.x=kπ-1,k∈Z,在区间(0,+∞)上有无数个零点.使乙为假.
故选D.
点评:要掌握好基本初等函数的单调性,以及函数零点个数的判定,用二分法求零点的近似值.
分析:①函数可用导数求出在(1,2)上是增函数,②函数是|log2x|与-
 的和函数,且两者在区间(1,2)上均是增函数,知
的和函数,且两者在区间(1,2)上均是增函数,知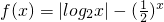 是增函数.③f(x)=0得cos(x+2)=cosx,在(0,+∞)上无数个零点.
是增函数.③f(x)=0得cos(x+2)=cosx,在(0,+∞)上无数个零点.解答:①f'(x)=4-
 ,在区间(1,2)f'(x)>0,f(x)在区间(1,2)上是增函数.使甲为真.f(x)的最小值是-1<0当x=
,在区间(1,2)f'(x)>0,f(x)在区间(1,2)上是增函数.使甲为真.f(x)的最小值是-1<0当x= 时取得.又f(1)=0,∴f(x)在区间(0,+∞)上恰有两个零点x1<
时取得.又f(1)=0,∴f(x)在区间(0,+∞)上恰有两个零点x1< ;x2=1. x1x2=x1<1,使乙为真.
;x2=1. x1x2=x1<1,使乙为真.②在区间(1,2),|log2x|=log2x,是增函数.-
 也是增函数,两者的和函数也是增函数.使甲为真.利用信息技术f(x)在区间(0,+∞)上恰有两个零点x1,x2;0<x1<
也是增函数,两者的和函数也是增函数.使甲为真.利用信息技术f(x)在区间(0,+∞)上恰有两个零点x1,x2;0<x1<
1<x2<2.使乙为真.
③f(x)=0得cos(x+2)=cosx.x+2=2kπ±x.x=kπ-1,k∈Z,在区间(0,+∞)上有无数个零点.使乙为假.
故选D.
点评:要掌握好基本初等函数的单调性,以及函数零点个数的判定,用二分法求零点的近似值.

练习册系列答案
相关题目