题目内容
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈M,且f(x+l)≥f(x),则称f(x)为M上的l高调函数.现给出下列命题:
①函数 为R上的1高调函数;
为R上的1高调函数;
②函数f(x)=lgx为(0,+∞)上的m(m>0)高调函数;
③函数f(x)=sin2x为R上的π高调函数;
④若函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).
其中正确命题的序号是________(写出所有正确命题的序号).
①②③④
分析:①函数 为减函数,存在负实数l使得对于任意x∈M(M⊆D),有x+l∈M,且f(x+l)≥f(x),满足高调函数定义;
为减函数,存在负实数l使得对于任意x∈M(M⊆D),有x+l∈M,且f(x+l)≥f(x),满足高调函数定义;
②根据对数函数f(x)=lgx的图象可得对数函数为增函数,且满足高调函数定义,故f(x)=lgx为(0,+∞)上的m(m>0)高调函数;
③由正弦函数知函数f(x)=sin2x为R上的π高调函数;
④函数f(x)=x2为[-1,+∞)上m高调函数,只有[-1,1]上至少需要加2.
解答:函数f(x+l)=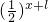 ,
, ,
,
要使f(x+l)≥f(x),需要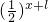 ≥
≥ 恒成立,只需l≤0;
恒成立,只需l≤0;
即存在l使得f(x+l)≥f(x)在R恒成立,
∴函数 是R上的1(l≤0)高调函数,故①正确;
是R上的1(l≤0)高调函数,故①正确;
∵f(x)=lgx为增函数,∴当m>0时,lg(x+m)≥lgx,
∴函数f(x)=lgx为(0,+∞)上的m(m>0)高调函数,故②正确;
∵sin2(x+π)≥sin2x,
∴函数f(x)=sin2x为R上的π高调函数,故③正确;
∵如果定义域为[1,+∞)的函数f(x)=x2为[-1,+∞)上m高调函数,
只有[-1,1]上至少需要加2,
那么实数m的取值范围是[2,+∞),故④正确,
综上,正确的命题序号是①②③④.
故答案为:①②③④
点评:此题属于新定义的题型,涉及的知识有:函数单调性的判断与证明,以及基本初等函数的性质,其中认真审题,弄清新定义的本质,找到判断的标准是解本题的关键.
分析:①函数
 为减函数,存在负实数l使得对于任意x∈M(M⊆D),有x+l∈M,且f(x+l)≥f(x),满足高调函数定义;
为减函数,存在负实数l使得对于任意x∈M(M⊆D),有x+l∈M,且f(x+l)≥f(x),满足高调函数定义;②根据对数函数f(x)=lgx的图象可得对数函数为增函数,且满足高调函数定义,故f(x)=lgx为(0,+∞)上的m(m>0)高调函数;
③由正弦函数知函数f(x)=sin2x为R上的π高调函数;
④函数f(x)=x2为[-1,+∞)上m高调函数,只有[-1,1]上至少需要加2.
解答:函数f(x+l)=
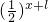 ,
, ,
,要使f(x+l)≥f(x),需要
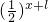 ≥
≥ 恒成立,只需l≤0;
恒成立,只需l≤0;即存在l使得f(x+l)≥f(x)在R恒成立,
∴函数
 是R上的1(l≤0)高调函数,故①正确;
是R上的1(l≤0)高调函数,故①正确;∵f(x)=lgx为增函数,∴当m>0时,lg(x+m)≥lgx,
∴函数f(x)=lgx为(0,+∞)上的m(m>0)高调函数,故②正确;
∵sin2(x+π)≥sin2x,
∴函数f(x)=sin2x为R上的π高调函数,故③正确;
∵如果定义域为[1,+∞)的函数f(x)=x2为[-1,+∞)上m高调函数,
只有[-1,1]上至少需要加2,
那么实数m的取值范围是[2,+∞),故④正确,
综上,正确的命题序号是①②③④.
故答案为:①②③④
点评:此题属于新定义的题型,涉及的知识有:函数单调性的判断与证明,以及基本初等函数的性质,其中认真审题,弄清新定义的本质,找到判断的标准是解本题的关键.

练习册系列答案
相关题目
 )与b=f(
)与b=f( )的大小关系为________.
)的大小关系为________. )与b=f(
)与b=f( )的大小关系为 .
)的大小关系为 . )与b=f(
)与b=f( )的大小关系为( ).
)的大小关系为( ).