题目内容
在等差数列{an}中，a1=3，其前n项和为Sn，等比数列{bn}的各项均为正数，b1=1，公比为q，且b2+S2=12，q=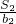
，求an与bn．
解：设等差数列{an}的公差为d，
∵等差数列{an}前n项和为Sn，数列{bn}为等比数列，且b2+S2=12，q=，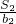
∴
…6分
即
…8分
解得
…10分
∴an=3+（n-1）•3=3n，bn=1•3n-1=3n-1…12分
分析：设等差数列{an}的公差为d，根据题意列出q，d的方程组，解之即可．
点评：本题考查等差数列与等比数列的通项公式，考查方程思想与运算能力，属于中档题．
∵等差数列{an}前n项和为Sn，数列{bn}为等比数列，且b2+S2=12，q=
，∴
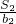…6分即
…8分解得
…10分∴an=3+（n-1）•3=3n，bn=1•3n-1=3n-1…12分
分析：设等差数列{an}的公差为d，根据题意列出q，d的方程组，解之即可．
点评：本题考查等差数列与等比数列的通项公式，考查方程思想与运算能力，属于中档题．
练习册系列答案
相关题目