题目内容
已知点P在直线x+3y-1=0上,点Q在直线x+3y+3=0上,PQ中点为M(x0,y0),
且y0≥x0+2,则 的取值范围为( )
的取值范围为( )
A. | B. |
C. | D. |
D
解析试题分析:根据题意作图如下
因为PQ中点为M,则点M的坐标满足方程x+3y+1=0,
又y0≥x0+2,则点M在直线y=x+2的左上部,
且由 得 N(-
得 N(- ,
, ),则kON=-
),则kON=- ,并且直线x+3y+1=0的斜率k=-
,并且直线x+3y+1=0的斜率k=- ,
,
而 可看作点M与原点O连线的斜率,故
可看作点M与原点O连线的斜率,故
 ,选D。
,选D。
考点:本题主要考查平面区域的概念,直线平行的性质,直线的斜率。
点评:典型题,本题具有一定综合性,关键是能分析出点M的坐标满足方程x+3y+1=0且分布在直线y=x+2的左上部,利用数形结合思想进一步分析求解得出“界点”。

练习册系列答案
相关题目
过点 且平行于直线
且平行于直线 的直线方程为( )
的直线方程为( )
A. | B. | C. | D. |
已知直线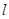 的方程为
的方程为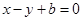
 ,则直线
,则直线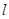 的倾斜角为( )
的倾斜角为( )
A.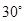 | B.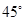 | C.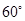 | D.与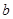 有关 有关 |
已知点 若直线
若直线 过点
过点 与线段
与线段 相交,则直线
相交,则直线 的斜率
的斜率 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
两直线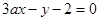 和
和 分别过定点A,B,则
分别过定点A,B,则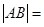 ( )
( )
A.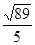 | B.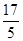 | C. | D.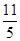 |
已知直线 平行,则k的值是( )
平行,则k的值是( )
| A. 3 | B.5 | C.3或5 | D.1或2 |
曲线 上的点到直线
上的点到直线 的最短距离是( )
的最短距离是( )
A. | B. | C. | D.0 |
已知两条直线 ,直线
,直线 ,则“
,则“ ”是“直线
”是“直线 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
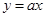 与
与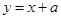 的是( )
的是( )