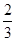题目内容
已知正四棱锥的侧棱长为2
,那么当该棱锥体积最大时,它的高为( )
| 3 |
分析:设出底面边长,求出正四棱锥的高,写出体积表达式,利用求导求得最大值时,高的值.
解答:解:设底面边长为a,则高h=
=
,
所以体积V=
a2h=
,
设y=12a4-
a6,则y′=48a3-3a5,
y′=48a3-3a5=0,
解可得a=4,
且当a>4时,y′≤0,函数y=12a4-
a6,在区间(4,+∞)是减函数;
当0<a<4时,y′>0,函数y=12a4-
a6,在区间(0,4)是增函数;
∴当a=4时,函数y=12a4-
a6,取得最大值,即此时体积最大,
此时h=
=2,
故选C.
(2
|
12-
|
所以体积V=
| 1 |
| 3 |
| 1 |
| 3 |
12a4-
|
设y=12a4-
| 1 |
| 2 |
y′=48a3-3a5=0,
解可得a=4,
且当a>4时,y′≤0,函数y=12a4-
| 1 |
| 2 |
当0<a<4时,y′>0,函数y=12a4-
| 1 |
| 2 |
∴当a=4时,函数y=12a4-
| 1 |
| 2 |
此时h=
12-
|
故选C.
点评:解决此类问题的关键是熟悉几何体的结构特征,正确记忆其体积公式并且能够灵活的利用导数解决最值问题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 A.
A. 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,则
的中点,则 所成的角的余弦值为(
)
所成的角的余弦值为(
)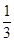 B.
B. C.
C. D.
D.
 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,则
的中点,则 所成的角的余弦值为( )
所成的角的余弦值为( ) B.
B.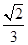 C.
C. D.
D.