题目内容
已知数列{an}满足a1=1, (n≥2),求数列{an}的通项公式.
(n≥2),求数列{an}的通项公式.
解:因为 =
=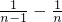 (n≥2),
(n≥2),
所以 ,
, ,
, ,…,
,…, ,
,
把以上各式加起来,得an-a1=(1- )+(
)+( )+(
)+(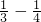 )+…+(
)+…+(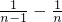 )=1-
)=1- (n≥2),
(n≥2),
所以an=2- (n≥2),
(n≥2),
当n=1时,a1=1适合上式,
所以an=2- (n∈N*).
(n∈N*).
分析:由递推公式可得 =
=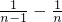 (n≥2),由此可得
(n≥2),由此可得 ,
, ,
, ,…,
,…, ,把各式加起来即可求得an,注意验证n=1时情况》
,把各式加起来即可求得an,注意验证n=1时情况》
点评:本题考查由数列递推公式求数列通项公式,已知形如an+1-an=f(n)求an,常用累加法解决.
 =
=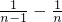 (n≥2),
(n≥2),所以
 ,
, ,
, ,…,
,…, ,
,把以上各式加起来,得an-a1=(1-
 )+(
)+( )+(
)+(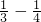 )+…+(
)+…+(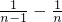 )=1-
)=1- (n≥2),
(n≥2),所以an=2-
 (n≥2),
(n≥2),当n=1时,a1=1适合上式,
所以an=2-
 (n∈N*).
(n∈N*).分析:由递推公式可得
 =
=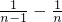 (n≥2),由此可得
(n≥2),由此可得 ,
, ,
, ,…,
,…, ,把各式加起来即可求得an,注意验证n=1时情况》
,把各式加起来即可求得an,注意验证n=1时情况》点评:本题考查由数列递推公式求数列通项公式,已知形如an+1-an=f(n)求an,常用累加法解决.

练习册系列答案
相关题目