题目内容
在△ABC中，角A、B、C的对边分别是a、b、c，且A为锐角，f(A)=2sin(
)sin(π+
)+cos2(
)-cos2(π+
).(1)求f(A)的最小值；
(2)若f(A)=-
,A+B=
,a=
，求b的大小.
解:(1)f(A)=-2cossin+sin2-cos2=-sinA-cosA=-sin(A+).
∵A为锐角，∴0＜A＜.∴
＜A+
＜
.
∴当A+
时，f(A)min=
.
(2)由题意知f(A)=
sin(A+
)=
,∴sin(A+
)=1.
又∵
＜A+
＜
，∴A+
=
.∴A=
.
又∵A+B=
，∴B=
.
由正弦定理
=
得b=
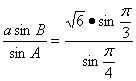=3.
练习册系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |