题目内容
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.(1)求证:BC⊥平面ACFE;
(2)当EM为何值时,AM∥平面BDF?证明你的结论;
(3)求二面角B-EF-D的平面角的余弦值.
【答案】分析:(1)由已知中梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,我们易求出AC⊥BC,结合已知中平面ACFE⊥平面ABCD,及平面与平面垂直的性质定理,即可得到BC⊥平面ACFE.
(2)以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,看出AM∥平面BDF等价于 与
与 、
、 共面,也等价于存在实数m、n,使
共面,也等价于存在实数m、n,使 =m
=m +n
+n ,根据向量之间的关系得到结论.
,根据向量之间的关系得到结论.
(3)要求两个平面所成的角,根据向量的加减运算做出平面的法向量,二面角B-EF-D的大小就是向量 与向量
与向量 所夹的角.根据向量的夹角做出结果.
所夹的角.根据向量的夹角做出结果.
解答:证明:(1)在梯形ABCD中,∵AB∥CD,
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE
解:(2)当 时,AM∥平面BDF,
时,AM∥平面BDF,
以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,则 ,
,
AM∥平面BDF? 与
与 、
、 共面,也等价于存在实数m、n,使
共面,也等价于存在实数m、n,使 =m
=m +n
+n ,
,
设 .
.
∵ =(-
=(- a,0,0),
a,0,0), ,0,0)
,0,0)
∴ =
= +
+ =(-
=(- at,0,0)
at,0,0)
又 =(
=( a,-
a,- a,-a),
a,-a), =(0,a,-a),
=(0,a,-a),
从而要使得: 成立,
成立,
需 ,解得
,解得 ∴当
∴当 时,AM∥平面BDF
时,AM∥平面BDF
(3B(0,a,0), ,
,
过D作DG⊥EF,垂足为G.令 =
= =λ(
=λ( a,0,0),
a,0,0),
 =
= +
+ =(
=( aλ,0,a),
aλ,0,a), =
= -
- =(
=( λa-
λa- a,
a, a,a)
a,a)
由 得,
得, ,
,
∴
∴ ,即
,即
∵BC⊥AC,AC∥EF,
∴BC⊥EF,BF⊥EF
∴二面角B-EF-D的大小就是向量 与向量
与向量 所夹的角.
所夹的角.
∵ =(0,a,-a)
=(0,a,-a)
cos< ,
, >=
>= ,即二面角B-EF-D的平面角的余弦值为
,即二面角B-EF-D的平面角的余弦值为 .
.

点评:本题考查用空间向量求平面间的夹角和线面之间的关系问题,本题解题的关键是建立适当的坐标系,写出要用的空间向量,把立体几何的理论推导变成数字的运算,这是新课标高考卷中常见的一种题目.
(2)以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,看出AM∥平面BDF等价于
 与
与 、
、 共面,也等价于存在实数m、n,使
共面,也等价于存在实数m、n,使 =m
=m +n
+n ,根据向量之间的关系得到结论.
,根据向量之间的关系得到结论.(3)要求两个平面所成的角,根据向量的加减运算做出平面的法向量,二面角B-EF-D的大小就是向量
 与向量
与向量 所夹的角.根据向量的夹角做出结果.
所夹的角.根据向量的夹角做出结果.解答:证明:(1)在梯形ABCD中,∵AB∥CD,
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE
解:(2)当
 时,AM∥平面BDF,
时,AM∥平面BDF,以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,则
 ,
,
AM∥平面BDF?
 与
与 、
、 共面,也等价于存在实数m、n,使
共面,也等价于存在实数m、n,使 =m
=m +n
+n ,
,设
 .
.∵
 =(-
=(- a,0,0),
a,0,0), ,0,0)
,0,0)∴
 =
= +
+ =(-
=(- at,0,0)
at,0,0)又
 =(
=( a,-
a,- a,-a),
a,-a), =(0,a,-a),
=(0,a,-a),从而要使得:
 成立,
成立,需
 ,解得
,解得 ∴当
∴当 时,AM∥平面BDF
时,AM∥平面BDF(3B(0,a,0),
 ,
,过D作DG⊥EF,垂足为G.令
 =
= =λ(
=λ( a,0,0),
a,0,0), =
= +
+ =(
=( aλ,0,a),
aλ,0,a), =
= -
- =(
=( λa-
λa- a,
a, a,a)
a,a)由
 得,
得, ,
,∴

∴
 ,即
,即
∵BC⊥AC,AC∥EF,
∴BC⊥EF,BF⊥EF
∴二面角B-EF-D的大小就是向量
 与向量
与向量 所夹的角.
所夹的角.∵
 =(0,a,-a)
=(0,a,-a)cos<
 ,
, >=
>= ,即二面角B-EF-D的平面角的余弦值为
,即二面角B-EF-D的平面角的余弦值为 .
.
点评:本题考查用空间向量求平面间的夹角和线面之间的关系问题,本题解题的关键是建立适当的坐标系,写出要用的空间向量,把立体几何的理论推导变成数字的运算,这是新课标高考卷中常见的一种题目.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
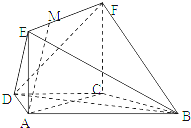 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.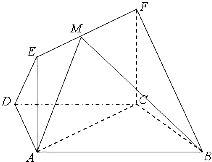 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.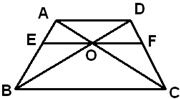 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.