题目内容
24、已知集合A={a,b,c},B={d,e},从A到B的不同映射有
8
;从B到A的不同映射有9
.分析:本题研究两个集合之间的映射种数,可以利用计数原理来求解其种数从A到B的不同映射可分为三步完成计数,从B到A的不同映射分两步完成计数.
解答:解:A中的每个元素的对应方式有2种,有三个元素,故可以分三步求A到B的不同映射的种数,即2×2×2=8
B中的每个元素的对应方式有3种,有2个元素,故可以分2步求B到A的不同映射的种数,即3×3=9
故答案为8,9
B中的每个元素的对应方式有3种,有2个元素,故可以分2步求B到A的不同映射的种数,即3×3=9
故答案为8,9
点评:本题考查映射的概念,考查两个集合之间映射的方式,求解本题可以利用列举法,最好选用计数原理,方便快捷,可迅速得出答案.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
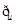 B)=R,则实数a的取值范围是 ( )
B)=R,则实数a的取值范围是 ( )