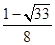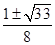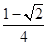题目内容
等差数列 和
和 的前
的前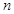 项和分别为
项和分别为 和
和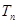 ,且
,且 ,则
,则 =( )
=( )
A. | B. | C. | D. |
D
解析试题分析:本题容易由等差数列的性质,联想等差数列 的前
的前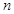 项和
项和 与项
与项 之间的关系:
之间的关系: ,所以我们有
,所以我们有 ,即
,即 ,当然
,当然 不可能直接利用已知条件
不可能直接利用已知条件 ,考虑到等差数列的前
,考虑到等差数列的前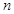 项和
项和 一定为
一定为 这种形式,故我们可以得出
这种形式,故我们可以得出 ,从而可设
,从而可设 ,(
,( 为常数)的形式,于是有:
为常数)的形式,于是有: .选D.
.选D.
考点:等差数列的前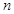 项和.
项和.

练习册系列答案
相关题目
在等差数列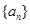 中,已知
中,已知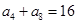 ,则该数列前11项的和
,则该数列前11项的和 等于( )
等于( )
| A.58 | B.88 | C.143 | D.176 |
已知等比数列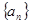 中,各项都是正数,且
中,各项都是正数,且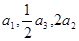 成等差数列,则
成等差数列,则 等于 ( )
等于 ( )
A.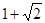 | B.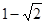 | C. | D.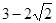 |
在等差数列 中,若
中,若 ,则
,则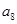 的值为( )
的值为( )
| A.20 | B.22 | C.24 | D.28 |
若等差数列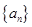 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知等差数列 的前13项之和为
的前13项之和为 ,则
,则 等于( )
等于( )
| A.—1 | B. | C. | D.1 |
数列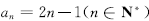 排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
| A.61 | B.62 | C.63 | D.64 |
已知数列{ }是公差为3的等差数列,且
}是公差为3的等差数列,且 成等比数列,则
成等比数列,则 等于( )
等于( )
| A.30 | B.27 | C.24 | D.33 |