题目内容
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A. ,2 ,2 | B. ,4 ,4 | C. , , | D. ,4 ,4 |
A
解析

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知函数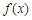 的定义域为R,若存在常数
的定义域为R,若存在常数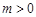 ,对任意
,对任意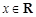 ,有
,有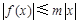 ,则称
,则称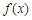
为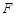 函数.给出下列函数:①
函数.给出下列函数:①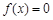 ; ②
; ②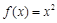 ; ③
; ③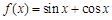 ;
;
④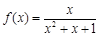 ; ⑤
; ⑤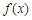 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数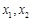 均
均
有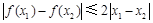 .其中是
.其中是 函数的序号为( )
函数的序号为( )
| A.①②④ | B.②③④ | C.①④⑤ | D.①②⑤ |
某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是( )
| A.118元 | B.105元 |
| C.106元 | D.108元 |
函数f(x)=|x-2|-lnx在定义域内零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知幂函数f(x)的图象过点P( ,2),则f(5)等于( )
,2),则f(5)等于( )
| A.10 | B.16 | C.25 | D.32 |
设a=22.5,b=2.50,c=( )2.5,则a,b,c的大小关系是( )
)2.5,则a,b,c的大小关系是( )
| A.a>c>b | B.c>a>b |
| C.a>b>c | D.b>a>c |
若函数f(x)= ,则函数f(x)的定义域是( )
,则函数f(x)的定义域是( )
| A.(1,+∞) | B.(0,1)∪(1,+∞) |
| C.(-∞,-1)∪(-1,0) | D.(-∞,0)∪(0,1) |
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)= ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
| A.(-∞,2] | B.[2,+∞) |
| C.[-2,+∞) | D.(-∞,-2] |
设 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |