题目内容
已知集合 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析: 时,因为
时,因为 ,所以
,所以 ;
;
反之,若 ,则必有
,则必有 ,所以
,所以 或
或 ,
,
故“ ”是“
”是“ ”的充分不必要条件.选
”的充分不必要条件.选 .
.
考点:集合的基本关系,充要条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题正确的是
A.“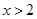 ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
B.命题“若 ,则 ,则 ”的否命题为“若 ”的否命题为“若 则 则 ” ” |
C.若 为假命题,则 为假命题,则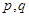 均为假命题 均为假命题 |
D.对于命题 : : ,使得 ,使得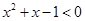 ,则 ,则 : : 均有 均有 |
已知命题 ,命题
,命题 ,则( )
,则( )
A.命题 是假命题 是假命题 | B.命题 是真命题 是真命题 |
C.命题 是假命题 是假命题 | D.命题 是真命题 是真命题 |
设 则
则 是“
是“ ”成立的 ( )
”成立的 ( )
| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既非充分也非必要条件 |
已知命题p:
 ≤0,则( )
≤0,则( )
A.p是假命题; p: p:  ≤0 ≤0 |
B.p是假命题; p: p:  >0 >0 |
C.p是真命题; p: p:  ≤0 ≤0 |
D.p是真命题; p: p:  >0 >0 |
命题“所有实数的平方是非负实数”的否定是( )
| A.所有实数的平方是负实数 |
| B.不存在一个实数,它的平方是负实数 |
| C.存在一个实数,它的平方是负实数 |
| D.不存在一个实数它的平方是非负实数 |
设命题p和q,在下列结论中,正确的是( )
①“p∧q”为真是“p∨q”为真的充分不必要条件;
②“p∧q”为假是“p∨q”为真的充分不必要条件;
③“p∨q”为真是“p”为假的必要不充分条件;
④“p”为真是“p∧q”为假的必要不充分条件.
| A.①② | B.①③ |
| C.②④ | D.③④ |
命题“存在一个无理数,它的平方是有理数”的否定是( )
| A.任意一个有理数,它的平方是有理数 |
| B.任意一个无理数,它的平方不是有理数 |
| C.存在一个有理数,它的平方是有理数 |
| D.存在一个无理数,它的平方不是有理数 |
“x2≥1”是“x≥1”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |