Question

已知等比数列的前3项和为168,a₂-a₅=42,求a₅,a₇的等比中项.

Answer 1

解:利用已知条件,列出关于首项a₁和公比q的方程组,求出a₁和q后,问题便得以解决.

    设该等比数列的首项为a₁,公比为q,由已知得

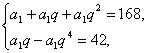
    即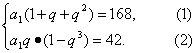

∵1-q³=(1-q)(1+q+q²),

∴由①②可得q(1-q)=.

∴q=.此时a₁==96.

    若G是a₅,a₇的等比中项,则应有G²=a₅·a₇=a₁²·q¹⁰=96²×()¹⁰=9.

∴a₅,a₇的等比中项是±3.