Question

已知抛物线C：x²=2py(p＞0)的焦点为F，A，B是抛物线C上异于坐标原点0的不同两点，抛物线C在点A，B处的切线分别为l₁，l₂，且l₁⊥l₂，l₁与l₂相交于点D。
(Ⅰ)求点D的纵坐标；
(Ⅱ)证明：A，B，F三点共线；
(Ⅲ)假设点D的坐标为（，-1），问是否存在经过A，B两点且与l₁，l₂都相切的圆，若存在，求出该圆的方程；若不存在，清说明理由。

Answer 1

(Ⅰ)解：设点A，B的坐标分别为(x₁，y₁)，(x₂，y₂)，
l₁，l₂分别是抛物线C在点A，B处的切线，
∴直线l₁的斜率为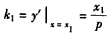，直线l₂的斜率为，
∵，
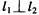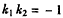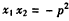∴，得，   ①
∵A，B是抛物线C上的点，
∴，
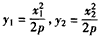∴直线l₁的方程为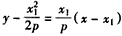，直线l₂的方程为，
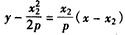由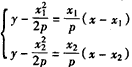，解得：，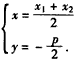
∴点D的纵坐标为。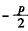
 (Ⅱ)证法一：∵F为抛物线C的焦点，
∴，
∴直线AF的斜率为，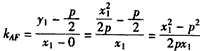
直线BF的斜率为，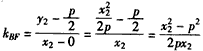
∵

，
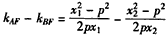
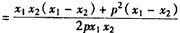
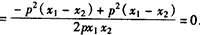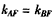∴，∴A，B，F三点共线。
证法二：∵F为抛物线C的焦点，
∴，
∴，，
∵，
∴，
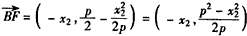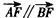∴A，B，F三点共线。
(Ⅲ)解：不存在，
证明如下：假设存在符合题意的圆，
设该圆的圆心为M，依题意，得MA⊥AD，MB⊥BD，且|MA|=|MB|，
由l₁⊥l₂，得AD⊥BD，
∴四边形MADB是正方形，∴|AD|=|BD|，
∵点D的坐标为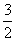（，-1），∴，即p=2，
把点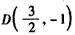代入直线l₁，得，
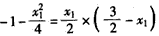解得：或，
∴点A的坐标为（4，4）或，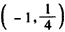
同理可求得点B的坐标为（4，4）或，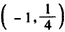
由于A，B是抛物线C上的不同两点，
不妨令，
∴，
，
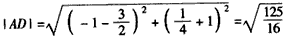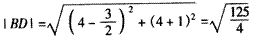∴|AD|≠|BD|，这与|AD|= |BD|矛盾，
∴经过A，B两点且与l₁，l₂都相切的圆不存在。