题目内容
已知等比数列{an}中,a1= ,公比q=
,公比q= .
.(I)Sn为{an}的前n项和,证明:Sn=
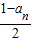
(II)设bn=log3a1+log3a2+…+log3an,求数列{bn}的通项公式.
【答案】分析:(I)根据数列{an}是等比数列,a1= ,公比q=
,公比q= ,求出通项公式an和前n项和Sn,然后经过运算即可证明.
,求出通项公式an和前n项和Sn,然后经过运算即可证明.
(II)根据数列{an}的通项公式和对数函数运算性质求出数列{bn}的通项公式.
解答:证明:(I)∵数列{an}为等比数列,a1= ,q=
,q=
∴an= ×
×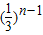 =
=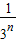 ,
,
Sn=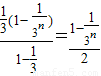
又∵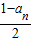 =
=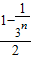 =Sn
=Sn
∴Sn=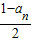
(II)∵an=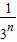
∴bn=log3a1+log3a2+…+log3an=-log33+(-2log33)+…-nlog33
=-(1+2+…+n)
=-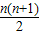
∴数列{bn}的通项公式为:bn=-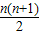
点评:本题主要考查等比数列的通项公式、前n项和以及对数函数的运算性质.
 ,公比q=
,公比q= ,求出通项公式an和前n项和Sn,然后经过运算即可证明.
,求出通项公式an和前n项和Sn,然后经过运算即可证明.(II)根据数列{an}的通项公式和对数函数运算性质求出数列{bn}的通项公式.
解答:证明:(I)∵数列{an}为等比数列,a1=
 ,q=
,q=
∴an=
 ×
×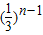 =
=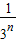 ,
,Sn=
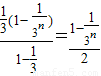
又∵
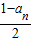 =
=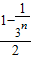 =Sn
=Sn∴Sn=
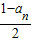
(II)∵an=
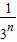
∴bn=log3a1+log3a2+…+log3an=-log33+(-2log33)+…-nlog33
=-(1+2+…+n)
=-
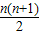
∴数列{bn}的通项公式为:bn=-
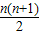
点评:本题主要考查等比数列的通项公式、前n项和以及对数函数的运算性质.

练习册系列答案
相关题目