题目内容
(本题满分14分
)设数列 的前
的前 项和为
项和为 ,
, ,当
,当 时,
时, .
.
(Ⅰ)若 ,求
,求 及
及 ;
;
(Ⅱ)求 的通项公式.
的通项公式.
)设数列
 的前
的前 项和为
项和为 ,
, ,当
,当 时,
时, .
.(Ⅰ)若
 ,求
,求 及
及 ;
;(Ⅱ)求
 的通项公式.
的通项公式.解:(Ⅰ)在 中取
中取 得,
得, ,
, . ---------2分
. ---------2分
由 得
得 相减可得
相减可得 ,即当
,即当 时
时
 .
.
可见, . ----------------4分
. ----------------4分

 ---------------6分
---------------6分
注:只写结果扣1分.
(Ⅱ)由 得
得 相减可得
相减可得 ,即当
,即当 时
时
 . -----------------9分
. -----------------9分
其中,
若 ,则由
,则由 知第二项之后是公差为
知第二项之后是公差为 的等差数列,但
的等差数列,但 ,故
,故 是等差数列,
是等差数列,
若 ,则
,则
若 ,
, ,则由
,则由 可得
可得
于是当 时,
时, 是一个公比为
是一个公比为 的等比数列 -----------------12分
的等比数列 -----------------12分

 即
即 (
( ).
).
 也适合上式,故
也适合上式,故 的通项公式为
的通项公式为 . ------------14分
. ------------14分
 中取
中取 得,
得, ,
, . ---------2分
. ---------2分由
 得
得 相减可得
相减可得 ,即当
,即当 时
时 .
.可见,
 . ----------------4分
. ----------------4分
 ---------------6分
---------------6分注:只写结果扣1分.
(Ⅱ)由
 得
得 相减可得
相减可得 ,即当
,即当 时
时 . -----------------9分
. -----------------9分其中,

若
 ,则由
,则由 知第二项之后是公差为
知第二项之后是公差为 的等差数列,但
的等差数列,但 ,故
,故 是等差数列,
是等差数列,
若
 ,则
,则
若
 ,
, ,则由
,则由 可得
可得
于是当
 时,
时, 是一个公比为
是一个公比为 的等比数列 -----------------12分
的等比数列 -----------------12分
 即
即 (
( ).
). 也适合上式,故
也适合上式,故 的通项公式为
的通项公式为 . ------------14分
. ------------14分略

练习册系列答案
相关题目
 ,
, 为前n项和,且
为前n项和,且 ,则
,则 取最小值时,n的值为___
取最小值时,n的值为___ 中,
中, 的值是
的值是 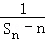 ,若C1+C2+C3+…+Cn≥m2﹣
,若C1+C2+C3+…+Cn≥m2﹣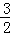 对任意正整数n恒成立,求实数m 的取值范围.
对任意正整数n恒成立,求实数m 的取值范围. 中,已知
中,已知 ,
, ,则它的前
,则它的前 项和
项和 ★ .
★ . , 则数列的通项
, 则数列的通项 =__
=__  则
则
 凸
凸 边形各内角成等差数列,公差
边形各内角成等差数列,公差 10°,最小内角为100°,则
10°,最小内角为100°,则 ( )
( )