题目内容
已知函数f(x)=x3-ax2+3x(Ⅰ)若函数f(x)在x∈[1，+∞)上是增函数，求实数a的取值范围；
(Ⅱ)若x=3是函数f(x)的极值点，设m＞1，求函数f(x)在[1，m]上的最小值和最大值．
答案：解：(Ⅰ)依题意得f′(x)=3x2-2ax+3
欲使函数f(x)在x∈[1，+∞)是增函数，
仅须或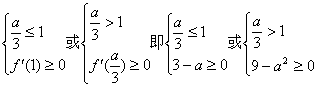
解之得 a≤3
故若f(x)在x∈[1，+∞)是增函数，实数a的取值范围为(-∞，3]
(Ⅱ)由(Ⅰ)得f′(x)=3x2-2ax+3，且x=3是f(x)的极值点，所以f′(3)=0
且30-6a=0，所以a=5
于是f′(x)=3x2-10x+3=3(x-3)(x
)，
∴函数f(x)的另一个极值点为x=
所以，在区间(1，3)上f′(x)＜0，f(x)是减函数；
在区间(3，+∞)上f′(x)＞0，f(x)是增函数
(ⅰ)当1＜m≤3时，f(x)的最小值为f(m)=m3-5m2+3m，
最大值为f(1)=-1
(ⅱ)令f(m)=f(1)，即m3-5m2+3m=-1
∴(m-1)(m2-4m-1)=0，
解得m=2+
，m=2-
(舍)，m=1(舍)
即当3＜m≤2+
时，
f(x)的最小值为f(3)=-9，最大值为f(1)=-1(11分)
(ⅱ)当m＞2+
时，f(x)的最小值为f(3)=-9，
最大值为f(m)=m3-5m2+3m
练习册系列答案
名校课堂系列答案
相关题目