题目内容
(12分)已知过点A(0,1)且斜率为 的直线
的直线 与圆C:
与圆C: 相交于M、N两点。
相交于M、N两点。
(1)求实数 的取值范围
的取值范围
(2)求证: 为定值
为定值
(3)若O为坐标原点,且 ,求K值。
,求K值。
(1) ,(2)
,(2) ,(3)
,(3)
【解析】
试题分析:直线与圆相交于两点,方法有两种(1)联立方程组利用判别式大于零,(2)圆心到直线的距离小于半径,第二步和第三步可采用设而不求思想,联立方程组减元后化为关于 的一元二次方程,首先满足
的一元二次方程,首先满足 ,然后利用根与系数关系写出
,然后利用根与系数关系写出 ,最后依据题意求解.
,最后依据题意求解.
试题解析:(1)由 ,把(1)代入(2)得:
,把(1)代入(2)得:

由△
 ,解得
,解得
(2)设 ,则
,则 ,
, ,
,





 为定值.
为定值.
(3)


 ,则
,则

 ,符合△
,符合△ 。
。
考点:1.直线和圆相交;2.设而不求思想;3.根与系数关系;平面向量数量积;

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 到原点的距离都相等.若复数
到原点的距离都相等.若复数 所对应的点为
所对应的点为 ,则复数
,则复数 的共轭复数所对应的点为( ).
的共轭复数所对应的点为( ).
 B.
B. C.
C. D.
D.
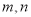 是两条不同的直线,
是两条不同的直线,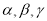 是三个不同的平面,给出下列命题,正确的是( )
是三个不同的平面,给出下列命题,正确的是( )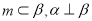 ,则
,则
 ,
,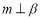 ,则
,则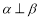
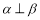 ,
, ,则
,则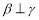
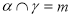 ,
, ,
,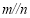 ,则
,则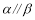 [
[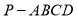 中,底面
中,底面 是菱形,
是菱形, 底面
底面 ,
, 是棱
是棱 上一点. 若
上一点. 若 ,则当
,则当 的面积为最小值时,直线
的面积为最小值时,直线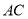 与平面
与平面 所成的角为( )
所成的角为( )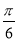 B.
B.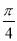 C.
C.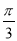 D.
D.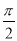
 与直线
与直线 互相垂直,则
互相垂直,则 的值为( )
的值为( ) B.
B.  C.
C. D.
D.
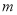 、
、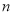 是两条不重合的直线,
是两条不重合的直线,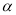 、
、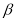 、
、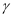 是三个两两不重合的平面,给出下列命题:
是三个两两不重合的平面,给出下列命题: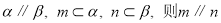 ;
;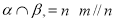 ,则
,则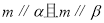
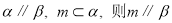 ;
;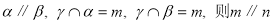 ;其中正确的命题是________
;其中正确的命题是________ 上有且有两个点到直线
上有且有两个点到直线 0的距离为1,则半径
0的距离为1,则半径 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 极大值为 .
极大值为 . :
: (
( 为正整数),下列四个命题:
为正整数),下列四个命题: