题目内容
【题目】若点O在![]() 内,且满足
内,且满足![]() ,设
,设![]() 为
为![]() 的面积,
的面积, ![]() 为
为![]() 的面积,则
的面积,则![]() =________.
=________.
【答案】![]()
【解析】由![]() ,可得:
,可得: ![]()
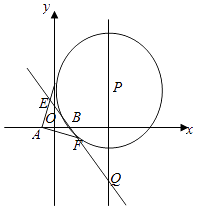
延长OA,OB,OC,使OD=2OA,OE=4OB,OF=3OC,
如图所示:

∵2![]() +3
+3![]() +4
+4![]() =
=![]() ,
,
∴![]() ,
,
即O是△DEF的重心,
故△DOE,△EOF,△DOF的面积相等,
不妨令它们的面积均为1,
则△AOB的面积为![]() ,△BOC的面积为
,△BOC的面积为![]() ,△AOC的面积为
,△AOC的面积为![]() ,
,
故三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() :
: ![]() :
: ![]() =3:2:4,
=3:2:4,
![]() .
.
故答案为: ![]() .
.
点睛:本题考查的知识点是三角形面积公式,三角形重心的性质,平面向量在几何中的应用,注意重要结论:点O在![]() 内,且满足
内,且满足![]() ,
, ![]() 则三角形△AOB,△BOC,△AOC的面积之比依次为:
则三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() .
.
【题型】填空题
【结束】
16
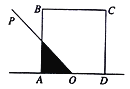
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).
【答案】①②
【解析】试题分析:①:如图,当![]() 时,
时, ![]() 与
与![]() 相交于点
相交于点![]() ,∵
,∵![]() ,则
,则![]() ,
,
∴![]() ,∴①正确;②:由于对称性,
,∴①正确;②:由于对称性, ![]() 恰好是正方形的面积,
恰好是正方形的面积,
∴![]() ,∴②正确;③:显然
,∴②正确;③:显然![]() 是增函数,∴
是增函数,∴![]() ,∴③错误.
,∴③错误.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目