Question

已知函数f（x）=ax²+bx+c满足：f（1）=3，且f（x）在R上为奇函数．
（1）求函数f（x）的解析式；
（2）设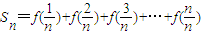，若不等式对n∈N⁺恒成立，求实数m的取值范围；
（3）若数列{a_n}，{b_n}满足：a₁=1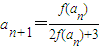，；b₁=1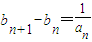，，记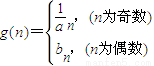，问是否存在k∈N，使g（k+1）=2g（k）成立，若存在，求出k值；若不存在，说明理由．

Answer 1

【答案】分析：（1）要求函数f（x）的解析式，只需找到关于a，b，c的三个方程，解方程组即可．由题意可由f（1）=3，且f（x）在R上为奇函数得．
（2）先用等差数列前n项和公式求S_n，得，S_n=，这时不等式可化为，在用作差法解不等式即可．
（3）分别用构造法和累加法求数列{a_n}，{b_n}的通项公式，再代入，然后假设存在k∈N，使g（k+1）=2g（k）成立，分k为奇数和偶数时求k的值．
解答：解：（1）由题意的，f（1）=a+b-c=3，f（-x）=f（x）对任意x∈R都成立，得f（x）=3x．
（2）=3（+…+）=（1+n），
∵化为，即对任意n∈N⁺恒成立，显然m≤0不成立．
当m＞0时，mⁿ＞0，
∴对任意n∈N⁺恒成立，
∴m＞对任意n∈N⁺恒成立．而的最大值为，
∴m＞．
（3）由a₁=1，，可得，
∴数列{}是首项为1，公差为2的等差数列，∴=2n-1．
由b₁=1，，用累加法可得b_n=（n-1）²+1，
∴=，
 当k为奇数时，g（k+1）=2g（k），（k+1-1）²+1=2（2k+1）得，k=1或k=3．
当k为偶数时，2k²-6k+3=0无偶数解．
综上，存在k=1或k=3满足条件．
点评：本题是数列，函数，不等式的综合应用，考查面广，须认真审题，找到个知识点的突破口．