题目内容
正四面体ABCD的棱长为1，棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 .
解析：如图，当四面体C—ABD绕AB进行旋转时，当CD垂直于平面α时，此时在α内的射影面积最小，等价于E在CD上移动时，当E为CD中点时，设F为AB中点，EF⊥AB.此时EF为异面直线AB与CD的公垂线，是CD上点的到AB距离最短的点，EF=
.∴
=
×1×
=
;当CD∥α时，四面体ABCD的射影为A′C′B′D′为正方形，对角A′B′=C′D′=1,此时面积最大.?
∵1为高是最大的，∴SA′C′B′D′=
×1×1=
.?
∴射影面积的取值范围为［
，
］.
答案：［
, 
］.
练习册系列答案
相关题目
正四面体ABCD的棱长为1，G是△ABC的中心，M在线段DG上，且∠AMB=90°，则GM的长为（ ）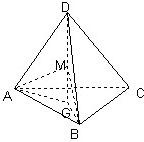
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2012•温州一模）如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为4，C在平面α内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（ ）