题目内容
甲袋中装有白球3个,黑球5个,乙袋内装有白球4个,黑球6个,现从甲袋内随机抽取一个球放入乙袋,充分掺混后再从乙袋内随机抽取一球放入甲袋,则甲袋中的白球没有减少的概率为
- A.

- B.

- C.

- D.

B
分析:甲袋中白球没有减少的两种情形;一是从甲袋中取出的球为黑球,此时不论从乙袋中取何种球放回甲袋,甲袋中的白球不会减少,另一种情形为从甲袋中取出的球是白球,放入乙袋,并由乙袋取白球放入甲.
解答:甲袋中白球没有减少的两种情形;一是从甲袋中取出的球为黑球,记作事件E,
此时不论从乙袋中取何种球放回甲袋,甲袋中的白球不会减少,
另一种情形为从甲袋中取出的球是白球,放入乙袋,此事件用F1表示,
并由乙袋取白球放入甲,用F2表示,
令F=F1F2.
则所求事件为E∪F,且E与F互斥,
显然P(E)= ,
,
下面计算P(F),记F1为由甲袋取出白球(不放入乙袋),
F2为当乙袋内有5个白球,6个黑球时取出一球为白球,
则显然有P(F1F2)=P(F1′F2′).
而F1′与F2′独立,故P(F1′F2′)= •
•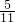 .
.
∴P(E∪F)=P(E)+P(F)= +
+ •
•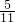 =
=
故选B.
点评:本题关键是看清题意,考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.
分析:甲袋中白球没有减少的两种情形;一是从甲袋中取出的球为黑球,此时不论从乙袋中取何种球放回甲袋,甲袋中的白球不会减少,另一种情形为从甲袋中取出的球是白球,放入乙袋,并由乙袋取白球放入甲.
解答:甲袋中白球没有减少的两种情形;一是从甲袋中取出的球为黑球,记作事件E,
此时不论从乙袋中取何种球放回甲袋,甲袋中的白球不会减少,
另一种情形为从甲袋中取出的球是白球,放入乙袋,此事件用F1表示,
并由乙袋取白球放入甲,用F2表示,
令F=F1F2.
则所求事件为E∪F,且E与F互斥,
显然P(E)=
 ,
,下面计算P(F),记F1为由甲袋取出白球(不放入乙袋),
F2为当乙袋内有5个白球,6个黑球时取出一球为白球,
则显然有P(F1F2)=P(F1′F2′).
而F1′与F2′独立,故P(F1′F2′)=
 •
•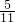 .
.∴P(E∪F)=P(E)+P(F)=
 +
+ •
•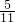 =
=
故选B.
点评:本题关键是看清题意,考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
甲袋中装有白球3个,黑球5个,乙袋内装有白球4个,黑球6个,现从甲袋内随机抽取一个球放入乙袋,充分掺混后再从乙袋内随机抽取一球放入甲袋,则甲袋中的白球没有减少的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|















