题目内容
已知△ABC不是直角三角形。
（1）证明：tanA+tanB+tanC=tanAtanBtanC；
（2）若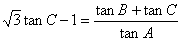
，且sin2A，sin2B，sin2C的倒数成等差数列，求
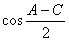的值。
（1）证明：tanA+tanB+tanC=tanAtanBtanC；
（2）若
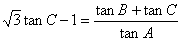，且sin2A，sin2B，sin2C的倒数成等差数列，求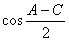的值。解：（1）A+B+C=π，A+B=π-C，两边取正切，tan （A+B）=tan（π-C）
。
（2）依题意，
由（1）知
∴
又
∴
即
将
代入得
3cos（A-C） =1+2cos（2A-2C）=4cos2（A-C）-1
4cos2（A-C）-3cos（A-C）-1=0，
于是cos（A-C）=1（此时△ABC为等边三角形）或
由于
∴
或
。
。（2）依题意，
由（1）知
∴
又
∴
即
将
代入得3cos（A-C） =1+2cos（2A-2C）=4cos2（A-C）-1
4cos2（A-C）-3cos（A-C）-1=0，
于是cos（A-C）=1（此时△ABC为等边三角形）或
由于
∴
或。
练习册系列答案
阅读快车系列答案
相关题目
已知△ABC的三个内角A、B、C所对边分别为a、b、c，则“c=acosB”是“△ABC为直角三角形”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．