题目内容
在△ABC中，AB=2
，AC=2，C=60°，则BC= ．
【答案】分析：利用余弦定理列出关系式，将各自的值代入计算即可求出BC的长．
解答：解：∵AB=c=2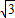
，AC=b=2，cosC=
，
∴由余弦定理得：c2=a2+b2-2abcosC，即12=a2+4-2a，
解得：a=4或a=-2（舍去），
则BC=a=4．
故答案为：4
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
解答：解：∵AB=c=2
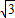，AC=b=2，cosC=，∴由余弦定理得：c2=a2+b2-2abcosC，即12=a2+4-2a，
解得：a=4或a=-2（舍去），
则BC=a=4．
故答案为：4
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目