Question

正三棱柱ABC-A₁B₁C₁中，AB=2，D是AC中点，且AB₁⊥BC₁
（Ⅰ）求侧棱AA₁的长；
（Ⅱ）求二面角D-BC₁-C的余弦值．

Answer 1

（Ⅰ）证明：取A₁B₁中点E，连接BC₁，EC₁，
∵ABC-A₁B₁C₁是正三棱柱，∴AB₁⊥EC₁
∵AB₁⊥BC₁，BC₁∩EC₁=C₁，
∴AB₁⊥平面BEC₁，∴AB₁⊥BE
∴△ABB₁∽△BB₁E
∴
∵AB=2，∴
∴    
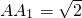
（Ⅱ）解：过D做DO⊥BC，垂足为O，过O做OG⊥BC₁，垂足为G，连接DG，则DG⊥BC₁，
∴∠OGD为二面角D-BC₁-C的平面角
在△CBC₁中，由等面积可得OG==
∵OD==
∴∠OGD=45°
∴二面角D-BC₁-C的余弦值为．
分析：（Ⅰ）取A₁B₁中点E，连接BC₁，EC₁，可得△ABB₁∽△BB₁E，从而可求侧棱AA₁的长；
（Ⅱ）过D做DO⊥BC，垂足为O，过O做OG⊥BC₁，垂足为G，连接DG，则DG⊥BC₁，故∠OGD为二面角D-BC₁-C的平面角，计算OD，OG，即可求得结论．
点评：本题考查面面角，考查侧棱长的计算，考查学生分析解决问题的能力，属于中档题．