题目内容
2. 在正方体ABCD-A1B1C1D1中,EF分别是棱AA1,A1C1的中点,求:
在正方体ABCD-A1B1C1D1中,EF分别是棱AA1,A1C1的中点,求:(1)CE与平面ABCD所成角的余弦值;
(2)EF与平面ABCD所成角的大小.
分析 (1)首先根据已知条件,指出线面的夹角,进一步利用解直角三角形知识求出结果.
(2)指出线面的夹角,进一步利用解直角三角形知识求出结果.
解答 解:(1)在正方体ABCD-A1B1C1D1中,设棱长为2,
E、F分别是棱AA1,A1D1的中点,连接AC,
由于:AE⊥平面ABCD,
所以:∠ECA就是直线CE与平面ABCD所成角,
则:$AC=2\sqrt{2}$,AE=1
利用勾股定理解得:$CE=\sqrt{{AC}^{2}+{AE}^{2}}$=3
所以:cos∠ECA=$\frac{AC}{CE}=\frac{2\sqrt{2}}{3}$
(2)E、F分别是棱AA1,A1D1的中点,
所以:△A1EF为等腰三角形.
EF与平面ABCD所成角,即EF与平面A1B1C1D1所成的角.
EA⊥平面ABCD,
平面ABCD∥平面A1B1C1D1
所以:∠EFA1就是EF与平面ABCD所成角.
由于△A1EF为等腰三角形,
所以:∠EFA1=45°
即:EF与平面ABCD所成角的大小为45°.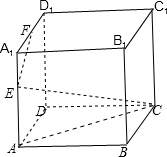
点评 本题考查的知识要点:线面的夹角问题,解直角三角形知识的应用.

练习册系列答案
相关题目
12.已知角α的终边过点(2,1),则sin2α等于( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |