题目内容
已知函数 ,其中a是大于0的常数
,其中a是大于0的常数
(1)求函数f(x)的定义域;
(2)当a∈(1,4)时,求函数f(x)在[2,+∞)上的最小值;
(3)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围.
解:(1)由 得,
得,
解得a>1时,定义域为(0,+∞)
a=1时,定义域为{x|x>0且x≠1},
0<a<1时,定义域为 或
或 }
}
(2)设 ,当a∈(1,4),x∈[2,+∞)时,
,当a∈(1,4),x∈[2,+∞)时,
 恒成立,
恒成立,
∴ 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,
∴ 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,
∴ 在[2,+∞)上的最小值为
在[2,+∞)上的最小值为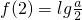 ;
;
(3)对任意x∈[2,+∞)恒有f(x)>0,
即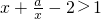 对x∈[2,+∞)恒成立
对x∈[2,+∞)恒成立
∴a>3x-x2,而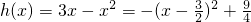 在x∈[2,+∞)上是减函数,
在x∈[2,+∞)上是减函数,
∴h(x)max=h(2)=2,∴a>2
分析:(1)求函数f(x)的定义域,就是)求 ,可以通过对a分类讨论解决;
,可以通过对a分类讨论解决;
(2)可以构造函数 ,当a∈(1,4)时通过导数法研究g(x)在[2,+∞)上的单调性,再利用复合函数的性质可以求得f(x)在[2,+∞)上的最小值;
,当a∈(1,4)时通过导数法研究g(x)在[2,+∞)上的单调性,再利用复合函数的性质可以求得f(x)在[2,+∞)上的最小值;
(3)对任意x∈[2,+∞)恒有f(x)>0,即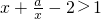 对x∈[2,+∞)恒成立,转化为a是x的函数,即可求得a的取值范围.
对x∈[2,+∞)恒成立,转化为a是x的函数,即可求得a的取值范围.
点评:本题考查函数恒成立问题,(1)着重考查分类讨论思想;(2)着重考查复合函数的函数单调性质求最值,方法为导数法;(3)着重考查分离参数法,是一道好题.
 得,
得,
解得a>1时,定义域为(0,+∞)
a=1时,定义域为{x|x>0且x≠1},
0<a<1时,定义域为
 或
或 }
}(2)设
 ,当a∈(1,4),x∈[2,+∞)时,
,当a∈(1,4),x∈[2,+∞)时, 恒成立,
恒成立,∴
 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,∴
 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,∴
 在[2,+∞)上的最小值为
在[2,+∞)上的最小值为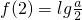 ;
;(3)对任意x∈[2,+∞)恒有f(x)>0,
即
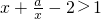 对x∈[2,+∞)恒成立
对x∈[2,+∞)恒成立∴a>3x-x2,而
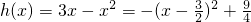 在x∈[2,+∞)上是减函数,
在x∈[2,+∞)上是减函数,∴h(x)max=h(2)=2,∴a>2
分析:(1)求函数f(x)的定义域,就是)求
 ,可以通过对a分类讨论解决;
,可以通过对a分类讨论解决;(2)可以构造函数
 ,当a∈(1,4)时通过导数法研究g(x)在[2,+∞)上的单调性,再利用复合函数的性质可以求得f(x)在[2,+∞)上的最小值;
,当a∈(1,4)时通过导数法研究g(x)在[2,+∞)上的单调性,再利用复合函数的性质可以求得f(x)在[2,+∞)上的最小值;(3)对任意x∈[2,+∞)恒有f(x)>0,即
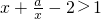 对x∈[2,+∞)恒成立,转化为a是x的函数,即可求得a的取值范围.
对x∈[2,+∞)恒成立,转化为a是x的函数,即可求得a的取值范围.点评:本题考查函数恒成立问题,(1)着重考查分类讨论思想;(2)着重考查复合函数的函数单调性质求最值,方法为导数法;(3)着重考查分离参数法,是一道好题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,其中a>0.
,其中a>0. 的单调区间;
的单调区间; 是曲线
是曲线 的切线,求实数a的值;
的切线,求实数a的值; ,求
,求 在区间
在区间 上的最大值(其中e为自然对的底数)。
上的最大值(其中e为自然对的底数)。 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.