题目内容
某黑箱中有大小、形状均相同的5只白球和3只黑球,活动参与者每次从中随机摸出一个球(取出后不放回),直到3只黑球全部被取出时停止摸球,求停止摸球后,箱中剩余的白球个数X的分布列及数学期望.
由题意知每次取一个球,
∴至少需3次,即X最大为5.有3只黑球,
当前3次取得的都是黑球时,X=5,
∴X可以取0,1,2,3,4,5.
当变量X是5时,表示第一次取出黑球,第二次取出也是黑球,第三次取出也是黑球,
根据相互独立事件同时发生的概率公式得到
P(X=5)=
×
×
=
;
P(X=4)=C
×
×
×
×
=
;
P(X=3)=C
×
×
×
×
×
=
;
P(X=2)=C
×
×
×
×
×
×
=
;
P(X=1)=C
×
×
×
×
×
×
×
=
;
P(X=0)=1-[P(X=5)+P(X=4)+P(X=3)+P(X=2)+P(X=1)]=
.
∴X的分布列如下:
EX=0×
+1×
+2×
+3×
+4×
+5×
=
.
∴至少需3次,即X最大为5.有3只黑球,
当前3次取得的都是黑球时,X=5,
∴X可以取0,1,2,3,4,5.
当变量X是5时,表示第一次取出黑球,第二次取出也是黑球,第三次取出也是黑球,
根据相互独立事件同时发生的概率公式得到
P(X=5)=
| 3 |
| 8 |
| 2 |
| 7 |
| 1 |
| 6 |
| 1 |
| 56 |
P(X=4)=C
| 13 |
| 5 |
| 8 |
| 3 |
| 7 |
| 2 |
| 6 |
| 1 |
| 5 |
| 3 |
| 56 |
P(X=3)=C
| 24 |
| 5 |
| 8 |
| 4 |
| 7 |
| 3 |
| 6 |
| 2 |
| 5 |
| 1 |
| 4 |
| 6 |
| 56 |
P(X=2)=C
| 35 |
| 5 |
| 8 |
| 4 |
| 7 |
| 3 |
| 6 |
| 3 |
| 5 |
| 2 |
| 4 |
| 1 |
| 3 |
| 10 |
| 56 |
P(X=1)=C
| 46 |
| 5 |
| 8 |
| 4 |
| 7 |
| 3 |
| 6 |
| 2 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 15 |
| 56 |
P(X=0)=1-[P(X=5)+P(X=4)+P(X=3)+P(X=2)+P(X=1)]=
| 21 |
| 56 |
∴X的分布列如下:
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
| 21 |
| 56 |
| 15 |
| 56 |
| 10 |
| 56 |
| 6 |
| 56 |
| 3 |
| 56 |
| 1 |
| 56 |
| 25 |
| 28 |

练习册系列答案
相关题目
 分的次数为
分的次数为 ,求
,求 ..
..








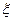 服从正态分布
服从正态分布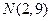 ,若
,若 ,则c=" ( " )
,则c=" ( " )