题目内容
如下图所示，等腰梯形ABCD的两底分别为AD=2，BC=1，∠BAD=45°,直线MN⊥AD交AD于M，交折线ABCD位于N，记AM=x,试将梯形ABCD于直线MN左侧的面积y表示为x的函数，并写出函数的定义域和值域，画出函数的图象.
解：过B、C分别作AD的垂线，垂足分别为H和G，则AH=
，AG=
，当M位于H左侧时，AM=x,MN=x.
∴y=S△AMN=
x·x=
x2(0≤x＜
).
当M位于H、G之间时，
y=
AH·BH+HM·MN
=
·
·
+（x-
）·
=
x-
（
≤x＜
）.
当M位于G、D之间时，y=S梯形ABCD-S△MDN
=
·
·（2+1）-
·（2-x）(2-x)
=-
x2+2x-
(
≤x≤2).
∴所求函数的关系式为
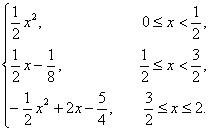
函数的图象如下图所示，函数的定义域为［0，2］，函数的值域为［0，
］.
练习册系列答案
相关题目
