题目内容
已知函数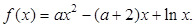
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点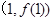 处的切线方程;
处的切线方程;
(Ⅱ)当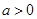 时,若
时,若 在区间
在区间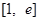 上的最小值为
上的最小值为 ,其中
,其中 是自然对数的底数,
是自然对数的底数,
求实数 的取值范围;
的取值范围;
(Ⅰ) (Ⅱ)
(Ⅱ)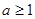 .
.
解析试题分析:
解题思路:(Ⅰ)求导,利用导数的几何意义求解;(Ⅱ)求导,讨论 的取值范围求函数的最值.
的取值范围求函数的最值.
规律总结:(1)导数的几何意义求切线方程: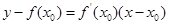 ;(2)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值.
;(2)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值.
试题解析:(Ⅰ)当 时,
时,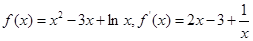 ,
,
因为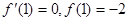 .所以切线方程是
.所以切线方程是
(Ⅱ)函数 的定义域是
的定义域是
当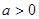 时,
时,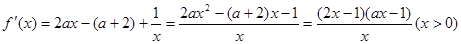
令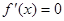 得
得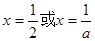
当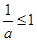 时,所以
时,所以 在
在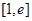 上的最小值是
上的最小值是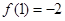 ,满足条件,于是
,满足条件,于是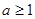 ;
;
②当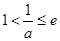 ,即
,即 时,
时, 在
在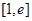 上的最小
上的最小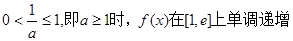
最小值 ,不合题意;
,不合题意;
③当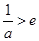 ,即
,即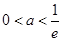 时,
时, 在
在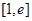 上单调递减,所以
上单调递减,所以 在
在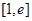 上的最小值是
上的最小值是 ,不合题意.
,不合题意.
综上所述有,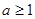 .
.
考点:1.导数的几何意义;2.利用导数研究函数的最值.

练习册系列答案
相关题目
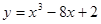
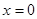 处的的切线方程;
处的的切线方程;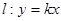 ,求切线方程.
,求切线方程.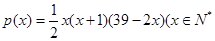 ,且
,且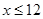 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
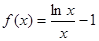 .
.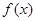 的单调性;
的单调性;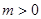 ,求
,求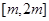 上的最大值;
上的最大值;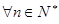 ,不等式
,不等式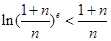 .
.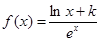 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线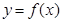 在点
在点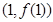 处的切线与x轴平行.
处的切线与x轴平行.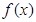 的单调区间;
的单调区间; 其中
其中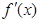 为
为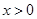 ,
,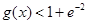 .
.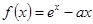 (
(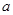 为常数)的图像与
为常数)的图像与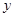 轴交于点
轴交于点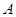 ,曲线
,曲线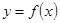 在点
在点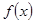 的极值;(2)证明:当
的极值;(2)证明:当 时,
时,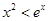 ;
;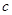 ,总存在
,总存在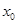 ,使得当
,使得当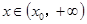 ,恒有
,恒有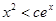 .
.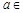 R,函数
R,函数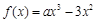 .
.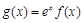 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围.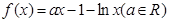 .
. 时,求函数
时,求函数 的单调区间;
的单调区间;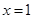 处取得极值,对
处取得极值,对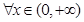 ,
, 恒成立,求实数
恒成立,求实数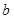 的取值范围;
的取值范围; 时,求证:
时,求证: .
.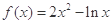 在其定义域内的一个子区间
在其定义域内的一个子区间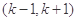 内不是单调函数,则实数
内不是单调函数,则实数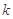 的取值范围是
的取值范围是