题目内容

函数f（x）=x³-3x²+5在区间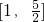 $数学公式$ 上的值域是 ________

[1，3]
分析：利用导数的运算法则求出导函数；求出导函数的根，判断根左右两边的符号，判断出函数的单调性，求出极值及两端点值比较出最值．
解答：f′（x）=3x²-6x
令f′（x）=0得x=0（舍）或x=2
当1＜x＜2时，f′（x）＜0；当 $\text{[math]}$ 时，f′（x）＞0
所以当x=2时，f（x）最小为f（2）=1
又当x=1时f（1）=3；当x= $\text{[math]}$ 时f（ $\text{[math]}$ ）= $\text{[math]}$
所以f（x）的值域为[1，3]
故答案为：[1，3]
点评：本题考查利用导数求函数的单调性、函数的极值、函数的最值．

练习册系列答案

汇测期末竞优系列答案

素质提优123系列答案

随堂练123系列答案

随堂新卷系列答案

堂堂清课堂8分钟小测系列答案

特级教师小学毕业升学系统总复习系列答案

提分计划单元期末系列答案

经纶学典提优作业本系列答案

题粹系列答案

高考模拟试题汇编系列答案

相关题目

已知函数f（x）=-x³+ax²+bx+c在（-∞，0）上是减函数，在（0，1）上是增函数，函数f（x）在R上有三个零点．
（1）求b的值；
（2）若1是其中一个零点，求f（2）的取值范围；
（3）若a=1，g（x）=f′（x）+3x²+lnx，试问过点（2，5）可作多少条直线与曲线y=g（x）相切？请说明理由．

（2007•东城区一模）已知函数f（x）=x³+ax²+bx+c，曲线y=f（x）在点x=1处的切线l不过第四象限且斜率为3，又坐标原点到切线l的距离为

时，y=f（x）有极值．
（1）求a，b，c的值；
（2）求y=f（x）在[-3，1]上的最大值和最小值．

（2013•宁波模拟）已知函数f（x）=x³+ax²-a²x+2，a∈R．
（1）若a＜0时，试求函数y=f（x）的单调递减区间；
（2）若a=0，且曲线y=f（x）在点A、B（A、B不重合）处切线的交点位于直线x=2上，证明：A、B 两点的横坐标之和小于4；
（3）如果对于一切x₁、x₂、x₃∈[0，1]，总存在以f（x₁）、f（x₂）、f（x₃）为三边长的三角形，试求正实数a的取值范围．

设函数f（x）=x³-3ax+b（a≠0），已知曲线y=f（x）在点（2，f（x））处在直线y=8相切．
（Ⅰ）求a，b的值；
（Ⅱ）求函数f（x）的单调区间与极值点．

对于函数f（x）=x³+ax²-x+1的极值情况，4位同学有下列说法：甲：该函数必有2个极值；乙：该函数的极大值必大于1；丙：该函数的极小值必小于1；丁：方程f（x）=0一定有三个不等的实数根．这四种说法中，正确的个数是（　　）