题目内容
对于函数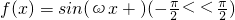 ,以下列四个命题中的两个为条件,余下的两个为结论,写出你认为正确的一个命题________.(序号表示)
,以下列四个命题中的两个为条件,余下的两个为结论,写出你认为正确的一个命题________.(序号表示)
①函数f (x)图象关于直线 对称;
对称;
②函数f (x)在区间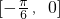 上是增函数;
上是增函数;
③函数f (x)图象关于点 对称;
对称;
④函数f (x)周期为π.
③④?①②或①④?②③
分析:分析四个条件可以判断出,④不可少,不然无法求出ω,②条件不能作为条件,由单调性不能求出∅,①或③条件都能与④结合求出函数的解析式,下依据解析式进行判断即可得出正确的命题.
解答:分析四个条件,只有④可以求出参数ω=2,条件②给出的是单调性,此条件不能用来求出参数∅
对于条件①,函数f (x)图象关于直线 对称故2×
对称故2× +φ=
+φ= 或2×
或2× +φ=-
+φ=- ,故φ=
,故φ= 或φ=
或φ=
∵- <φ<
<φ< ∴φ=
∴φ= ,即函数表达式为y=sin(2x+
,即函数表达式为y=sin(2x+ )可以证得②③是这个函数的特性.故①④?②③
)可以证得②③是这个函数的特性.故①④?②③
对于条件③函数f (x)图象关于点 对称,可得2×
对称,可得2× +φ=0或π故可以解得φ=
+φ=0或π故可以解得φ= 或φ=
或φ= ,同理可以得到函数的解析式为y=sin(2x+
,同理可以得到函数的解析式为y=sin(2x+ ),可以证得①②是这个函数的特性.故③④?①②
),可以证得①②是这个函数的特性.故③④?①②
综上知,应填①④?②③或③④?①②
点评:本题考查三角函数的图象与性质中的一种常 见题--(知点的坐标或图象的对称性求解析式)的解法,是高考试卷上的热门题型,解决此类问题关键是把握其规律,明确那种特征能求得那个参数的值.
分析:分析四个条件可以判断出,④不可少,不然无法求出ω,②条件不能作为条件,由单调性不能求出∅,①或③条件都能与④结合求出函数的解析式,下依据解析式进行判断即可得出正确的命题.
解答:分析四个条件,只有④可以求出参数ω=2,条件②给出的是单调性,此条件不能用来求出参数∅
对于条件①,函数f (x)图象关于直线
 对称故2×
对称故2× +φ=
+φ= 或2×
或2× +φ=-
+φ=- ,故φ=
,故φ= 或φ=
或φ=
∵-
 <φ<
<φ< ∴φ=
∴φ= ,即函数表达式为y=sin(2x+
,即函数表达式为y=sin(2x+ )可以证得②③是这个函数的特性.故①④?②③
)可以证得②③是这个函数的特性.故①④?②③对于条件③函数f (x)图象关于点
 对称,可得2×
对称,可得2× +φ=0或π故可以解得φ=
+φ=0或π故可以解得φ= 或φ=
或φ= ,同理可以得到函数的解析式为y=sin(2x+
,同理可以得到函数的解析式为y=sin(2x+ ),可以证得①②是这个函数的特性.故③④?①②
),可以证得①②是这个函数的特性.故③④?①②综上知,应填①④?②③或③④?①②
点评:本题考查三角函数的图象与性质中的一种常 见题--(知点的坐标或图象的对称性求解析式)的解法,是高考试卷上的热门题型,解决此类问题关键是把握其规律,明确那种特征能求得那个参数的值.

练习册系列答案
相关题目
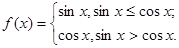 给出下列四个命题:
给出下列四个命题: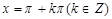 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;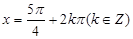 对称;
对称;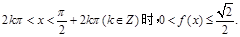
 给出下列四个命题:
给出下列四个命题: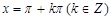 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;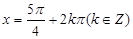 对称;
对称;