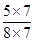题目内容
袋中有5个黑球和3个白球,从中任取2个球,则其中至少有1个黑球的概率是( )
分析:确定至少有1个黑球,包括1个黑球、2个黑球的方法数、袋中有5个黑球和3个白球,从中任取2个球,共有方法数,即可求得概率.
解答:解:至少有1个黑球,包括1个黑球、2个黑球,其方法数为
+
∵袋中有5个黑球和3个白球,从中任取2个球,
∴共有方法数为
∴至少有1个黑球的概率是
故选B.
| C | 1 5 |
| C | 1 3 |
| C | 2 5 |
| C | 0 3 |
∵袋中有5个黑球和3个白球,从中任取2个球,
∴共有方法数为
| C | 2 8 |
∴至少有1个黑球的概率是
| ||||||||
|
故选B.
点评:本题考查概率的计算,考查组合知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
A袋中有5个白球和3个黑球,从其中任取2个球,则取得二球颜色不相同的概率是( )
| A、0.357 | B、0.107 | C、0.646 | D、0.250 |
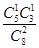 B.
B.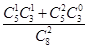
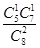 D.
D.